题目内容
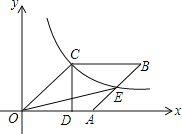
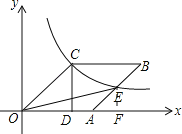
【题目】如图,已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数![]() 的图象经过点C,且与AB交于点E.若OD=2,则△OAE的面积为_____.
的图象经过点C,且与AB交于点E.若OD=2,则△OAE的面积为_____.
【答案】![]()
【解析】
过E作EF垂直于x轴,由OD的长得到C的横坐标,代入反比例解析式求出纵坐标,确定出CD的长,利用勾股定理求出OC的长,即为OA的长,设EF=AF=x,表示出E坐标,代入反比例解析式求出x的值,确定出EF的长,即可求出三角形OAE面积.
解:过点E作EF⊥x轴,交x轴于点F,
∵OD=2,即C横坐标为2,
∴把x=2代入反比例解析式得:y=2,即C(2,2),
∴CD=OD=2,即△OCD为等腰直角三角形,
∵四边形ABCO为菱形,
∴OC∥AB,OA=OC=2![]() ,
,
∴∠EAF=45°,
设EF=AF=x,则有OF=OA+AF=2![]() +x,
+x,
∴E(2![]() +x,x),
+x,x),
把E坐标代入反比例解析式得:x(2![]() +x)=4,
+x)=4,
解得:x=﹣![]() (负值舍去),
(负值舍去),
则△OAE面积S=![]() .
.
故答案为:![]()

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目