题目内容
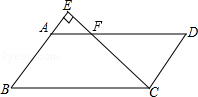
如图，在平行四边形ABCD中，过点C的直线CE⊥AB，垂足为E，若∠EAD=53°，则∠BCE的度数为【 】
| A．53° | B．37° | C．47° | D．123° |
B。
设CE与AD相交于点F。
∵在平行四边形ABCD中，过点C的直线CE⊥AB，∴∠E=90°，
∵∠EAD=53°，∴∠EFA=90°﹣53°=37°。∴∠DFC=37
∵四边形ABCD是平行四边形， ∴AD∥BC。
∴∠BCE=∠DFC=37°。故选B。
∵在平行四边形ABCD中，过点C的直线CE⊥AB，∴∠E=90°，
∵∠EAD=53°，∴∠EFA=90°﹣53°=37°。∴∠DFC=37
∵四边形ABCD是平行四边形， ∴AD∥BC。
∴∠BCE=∠DFC=37°。故选B。
练习册系列答案
相关题目
cm和16cm，绕它的对称中心旋转一周所扫过的面积是 
；旋转90度时，扫过的面积是 
中，
交
于
，交 
的延长线于
，若
，
厘米，则
厘米．
那么
= （用
表示）．
和
，则菱形的面积为S= 。