题目内容
(2013•永安市质检)(1)解不等式:
x-1>2x,并把解集在数轴上表示出来;

(2)如图2,已知E是平行四边形ABCD的边AB上的点,连接DE.
①在∠ABC的内部,作射线BM交线段CD于点F,使∠CBF=∠ADE;(要求:用尺规作图,保留作图痕迹,不写作法);
②在①的条件下,求证:△ADE≌△CBF.
| 3 | 2 |

(2)如图2,已知E是平行四边形ABCD的边AB上的点,连接DE.
①在∠ABC的内部,作射线BM交线段CD于点F,使∠CBF=∠ADE;(要求:用尺规作图,保留作图痕迹,不写作法);
②在①的条件下,求证:△ADE≌△CBF.
分析:(1)首先解出不等式,再利用数轴的出解集;
(2)①作∠CBF=∠ADE即可得出答案;
②利用在平行四边形ABCD中,∠A=∠C,AD=BC,进而利用三角形全等的判定定理得出即可.
(2)①作∠CBF=∠ADE即可得出答案;
②利用在平行四边形ABCD中,∠A=∠C,AD=BC,进而利用三角形全等的判定定理得出即可.
解答: 解:(1)
解:(1)
x-1>2x
解得:-
x>1,
则x<-2,
如图所示:
(2)①如图所示:∠CBF即为所求;
②∵在平行四边形ABCD中,∴∠A=∠C,AD=BC,
在△ADE和△CBF中
,
∴△ADE≌△CBF.
 解:(1)
解:(1)| 3 |
| 2 |
解得:-
| 1 |
| 2 |
则x<-2,
如图所示:
(2)①如图所示:∠CBF即为所求;
②∵在平行四边形ABCD中,∴∠A=∠C,AD=BC,
在△ADE和△CBF中
|
∴△ADE≌△CBF.
点评:此题主要考查了平行四边形的性质和全等三角形的判定以及不等式的解法等知识,熟练利用平行线的性质得出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
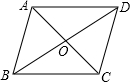 (2013•永安市质检)如图,四边形ABCD的对角线互相平分,请你添加一个条件,使它成为矩形,你添加的条件是
(2013•永安市质检)如图,四边形ABCD的对角线互相平分,请你添加一个条件,使它成为矩形,你添加的条件是 (2013•永安市质检)如图,菱形COAB的顶点B在y轴上,顶点C的坐标为(-3,2)?若反比例函数
(2013•永安市质检)如图,菱形COAB的顶点B在y轴上,顶点C的坐标为(-3,2)?若反比例函数