题目内容
【题目】如图,在△ABC中,∠C=90°,AC=4,BC=3,点P从点A出发,以每秒4个单位长度的速度沿折线AC-CB运动,到点B停止.当点P不与△ABC的顶点重合时,过点P作其所在直角边的垂线交AB 于点Q,再以PQ为斜边作等腰直角三角形△PQR,且点R与△ABC的另一条直角边始终在PQ同侧,设△PQR与△ABC重叠部分图形的面积为S(平方单位).点P的运动时间为t(秒).
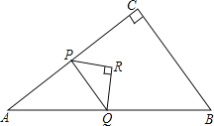
(1)求点P在AC边上时PQ的长,(用含t的代数式表示);
(2)求点R到AC、PQ所在直线的距离相等时t的取值范围;
(3)当点P在AC边上运动时,求S与t之间的函数关系式;
(4)直接写出点R落在△ABC高线上时t的值.
【答案】(1) 3t;(2) 0<t<1或t=![]() ;(3)s=-28t2+44t-16;(4)
;(3)s=-28t2+44t-16;(4)
【解析】
试题分析:(1)只需利用三角函数就可解决问题;
(2)可分点P在AC边上(图①)和点P在BC边上(图②)两种情况讨论:当点P在AC边上时,易得点R到AC、PQ所在直线的距离始终相等,从而可得0<t<1;当点P在BC边上时,易得PC=PQ,由此建立关于t的方程,就可解决问题;
(3)可分△PQR全部在△ABC内和△PQR部分在△ABC内两种情况讨论:当△PQR全部在△ABC内时,只需运用三角形的面积公式就可解决问题;当△PQR部分在△ABC内时,只需运用割补法就可解决问题;
(4)可分以下几种情况讨论:点R在AB的高CH上(如图④和图⑦)、点R在AC的高BC上(如图⑤)、点R在BC的高AC上(如图⑥),其中图④和图⑦可通过构造K型全等,并利用相似三角形的性质来解决问题,图5和图6可通过PQ=2PC来解决问题.
试题解析:(1)如图①,
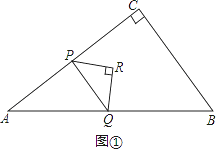
由题意可知AP=4t,
tanA=![]() ,
,
∴PQ=3t;
(2)①当点P在AC边上时,如图①.
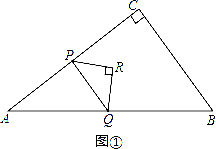
∵∠RPQ=45°,∠CPQ=90°,
∴∠CPR=45°=∠RPQ,
∴点R到直线AC、PQ距离相等,
此时0<t<1.
②当点P在BC边上时,过点R作RH⊥PQ于点H,如图②,
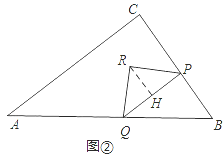
则有PC=4t-4,PB=7-4t,
∵tanB=![]() ,
,
∴PQ=![]() PB=
PB=![]() (7-4t).
(7-4t).
由题可得:RH=![]() PC.
PC.
∵RH=![]() PQ,
PQ,
∴PC=PQ,
∴4t-4=![]() (7-4t),
(7-4t),
解得:t=![]() .
.
综上所述:0<t<1或t=![]() ;
;
(3)①当0<t≤![]() 时,如图①.
时,如图①.
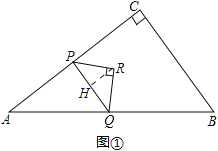
过点R作RH⊥PQ于点H,
S=![]() PQRH=
PQRH=![]() ×3t×
×3t×![]() =
=![]() t2.
t2.
②当![]() <t<1时,如图③.
<t<1时,如图③.
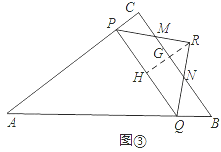
过点R作RH⊥PQ于点H,交BC于点G,
则有RG⊥MN,RH=![]() PQ=
PQ=![]() t,GH=PC=4-4t,
t,GH=PC=4-4t,
∴S=S△RPQ-S△RMN=![]() PQRH-
PQRH-![]() MNRH
MNRH
=RH2-RG2=(![]() t)2-[
t)2-[![]() t-(4-4t)]2
t-(4-4t)]2
=-28t2+44t-16;
(4)点R落在△ABC高线上时,t的值为![]() ,
,![]() ,
,![]() ,
,![]() .
.
可分以下几种情况讨论:如图④~⑦
①点P在AC上,且点R在AB的高CH上,如图④,
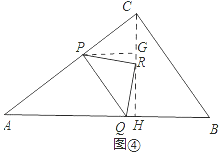
过点P作PG⊥CH于G,
易证△PGR≌△RHQ,则有PG=RH,GR=QH.
易求得AB=5,CH=![]() ,AH=
,AH=![]() ,BH=
,BH=![]() .
.
PC=4-4t,CG=![]() PC=
PC=![]() (4-4t),PG=
(4-4t),PG=![]() PC=
PC=![]() (4-4t),
(4-4t),
AQ=![]() AP=5t,QH=AH-AQ=
AP=5t,QH=AH-AQ=![]() -5t.
-5t.
根据CH=CG+GR+RH=CG+QH+PG=![]() ,得
,得
![]() (4-4t)+
(4-4t)+![]() -5t+
-5t+![]() (4-4t)=
(4-4t)=![]() ,
,
解得:t=![]() .
.
②点P在AC上,且点R在AC的高BC上,如图⑤
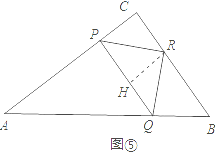
过点R作RH⊥PQ于H,
易得PQ=2RH=2PC,PQ=![]() AP=3t,PC=4-4t,
AP=3t,PC=4-4t,
∴3t=2(4-4t),
解得:t=![]() .
.
③点P在BC上,且点R在BC的高AC上,如图⑥,
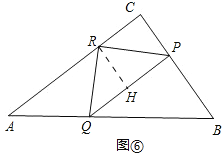
过点R作RH⊥PQ于H,
易得PQ=2RH=2PC,PQ=![]() PB=
PB=![]() (7-4t),PC=4t-4,
(7-4t),PC=4t-4,
∴![]() (7-4t)=2(4t-4),
(7-4t)=2(4t-4),
解得:t=![]() .
.
④点P在BC上,且点R在AB的高CH上,如图⑦,
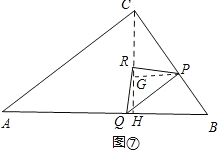
过点P作PG⊥CH于G,
易证△PGR≌△RHQ,则有PG=RH,GR=QH.
易证△CGP∽△CHB,
∴![]() .
.
∵BC=3,CH=![]() ,BH=
,BH=![]() ,CP=4t-4,
,CP=4t-4,
∴CG=![]() PC=
PC=![]() (4t-4),PG=
(4t-4),PG=![]() PC=
PC=![]() (4t-4),
(4t-4),
同理可得QB=![]() PB=
PB=![]() (7-4t),QH=QB-BH=
(7-4t),QH=QB-BH=![]() (7-4t)-
(7-4t)-![]() .
.
根据CH=CG+GH=CG+RH-RG=CG+PG-QH=![]() ,得
,得
![]() (4t-4)+
(4t-4)+![]() (4t-4)-[
(4t-4)-[![]() (7-4t)-
(7-4t)-![]() ]=
]=![]() ,
,
解得:t=![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x) | 1 | 2 | 3 | 4 | … |
座位数(y) | 50 | 53 | 56 | 59 | … |
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
