题目内容
(2010•闸北区二模)如图,在直角坐标平面内有点A(6,0),B(0,8),C(-4,0),点M、N分别为线段AC和射线AB上的动点,点M以2个单位长度/秒的速度自C向A方向作匀速运动,点N以5个单位长度/秒的速度自A向B方向作匀速运动,MN交OB于点P.(1)求证:MN:NP为定值;
(2)若△BNP与△MNA相似,求CM的长;
(3)若△BNP是等腰三角形,求CM的长.
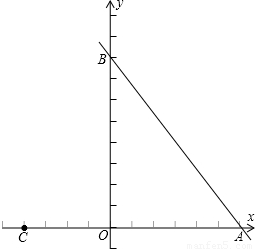
【答案】分析:(1)过点N作NH⊥x轴于点H,然后分两种情况进行讨论,综合两种情况,求得MN:NP为定值 .
.
(2)当△BNP与△MNA相似时,当点M在CO上时,只可能是∠MNB=∠MNA=90°,所以△BNP∽△MNA∽△BOA,所以 ,
,
所以 ,
, ,即
,即 ;当点M在OA上时,只可能是∠NBP=∠NMA,所以∠PBA=∠PMO,根据题意可以判定不成立,所以
;当点M在OA上时,只可能是∠NBP=∠NMA,所以∠PBA=∠PMO,根据题意可以判定不成立,所以 .
.
(3)由于等腰三角形的特殊性质,应分三种情况进行讨论,即BP=BN,PB=PN,NB=NP三种情况进行讨论.
解答:证明:(1)过点N作NH⊥x轴于点H,
设AN=5k,得:AH=3k,CM=2k,
①当点M在CO上时,点N在线段AB上时:
∴OH=6-3k,OM=4-2k,
∴MH=10-5k,
∵PO∥NH,
∴ ,
,
②当点M在OA上时,点N在线段AB的延长线上时:
∴OH=3k-6,OM=2k-4,∴MH=5k-10,
∵PO∥NH,
∴ ;
;
解:(2)当△BNP与△MNA相似时:
①当点M在CO上时,只可能是∠MNB=∠MNA=90°,
∴△BNP∽△MNA∽△BOA,∴ ,
,
∴ ,
, ,
, ,
,
②当点M在OA上时,只可能是∠NBP=∠NMA,
∴∠PBA=∠PMO,

∵
∴∠PBA≠∠PMO,矛盾∴不成立;
(3)∵ ,
, ,∴
,∴ ,
, ,
,
①当点M在CO上时,BN=10-5k,
(ⅰ)BP=BN, ,
, ,
, ;
;
(ⅱ)PB=PN,则∠PNB=∠PBN,∵∠PNB>∠BAC>∠PBN,矛盾,∴不成立;
(ⅲ)NB=NP,则∠NBP=∠NPB
∵∠NPB=∠MNH,∠NBP=∠ANH,∴∠MNH=∠ANH
又∵NH⊥MA,可证△MNA为等腰三角形,
∴MH=AH,∴10-5k=3k,∴ ,
, ;
;
②当点M在OA上时,BN=5k-10.
(ⅰ)BP=BN, ,
, ,
, ;
;
(ⅱ)PB=PN或NB=NP∵∠PBN>90°,∴不成立.
点评:本题主要是渗透分类思想,培养学生的严密性思维和解题方法:确定图形--分析图形--数形结合--解决问题.
 .
.(2)当△BNP与△MNA相似时,当点M在CO上时,只可能是∠MNB=∠MNA=90°,所以△BNP∽△MNA∽△BOA,所以
 ,
,所以
 ,
, ,即
,即 ;当点M在OA上时,只可能是∠NBP=∠NMA,所以∠PBA=∠PMO,根据题意可以判定不成立,所以
;当点M在OA上时,只可能是∠NBP=∠NMA,所以∠PBA=∠PMO,根据题意可以判定不成立,所以 .
.(3)由于等腰三角形的特殊性质,应分三种情况进行讨论,即BP=BN,PB=PN,NB=NP三种情况进行讨论.
解答:证明:(1)过点N作NH⊥x轴于点H,
设AN=5k,得:AH=3k,CM=2k,
①当点M在CO上时,点N在线段AB上时:
∴OH=6-3k,OM=4-2k,
∴MH=10-5k,
∵PO∥NH,
∴
 ,
,②当点M在OA上时,点N在线段AB的延长线上时:
∴OH=3k-6,OM=2k-4,∴MH=5k-10,
∵PO∥NH,
∴
 ;
;解:(2)当△BNP与△MNA相似时:
①当点M在CO上时,只可能是∠MNB=∠MNA=90°,
∴△BNP∽△MNA∽△BOA,∴
 ,
,∴
 ,
, ,
, ,
,②当点M在OA上时,只可能是∠NBP=∠NMA,
∴∠PBA=∠PMO,

∵

∴∠PBA≠∠PMO,矛盾∴不成立;
(3)∵
 ,
, ,∴
,∴ ,
, ,
,①当点M在CO上时,BN=10-5k,
(ⅰ)BP=BN,
 ,
, ,
, ;
;(ⅱ)PB=PN,则∠PNB=∠PBN,∵∠PNB>∠BAC>∠PBN,矛盾,∴不成立;
(ⅲ)NB=NP,则∠NBP=∠NPB
∵∠NPB=∠MNH,∠NBP=∠ANH,∴∠MNH=∠ANH
又∵NH⊥MA,可证△MNA为等腰三角形,
∴MH=AH,∴10-5k=3k,∴
 ,
, ;
;②当点M在OA上时,BN=5k-10.
(ⅰ)BP=BN,
 ,
, ,
, ;
;(ⅱ)PB=PN或NB=NP∵∠PBN>90°,∴不成立.
点评:本题主要是渗透分类思想,培养学生的严密性思维和解题方法:确定图形--分析图形--数形结合--解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
.
 .
.