题目内容
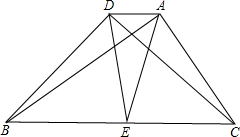 如图,若△ABC与△BCD都是直角三角形,∠BDC=∠BAC=Rt∠.点E是BC的中点,连接DE、AE、AD,求证:△ADE是等腰三角形.
如图,若△ABC与△BCD都是直角三角形,∠BDC=∠BAC=Rt∠.点E是BC的中点,连接DE、AE、AD,求证:△ADE是等腰三角形.分析:根据直角三角形斜边上的中线等于斜边的一半可得DE=
BC,AE=
BC,从而得到DE=AE,再根据等腰三角形的定义证明即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵∠BDC=∠BAC=Rt∠,点E是BC的中点,
∴DE=
BC,AE=
BC,
∴DE=AE,
∴△ADE是等腰三角形.
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
∴DE=AE,
∴△ADE是等腰三角形.
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形的判定,熟记性质并准确识图求出DE=AE是解题的关键.

练习册系列答案
相关题目
如图,若△ABC与△A'B'C'关于直线MN对称,BB'交MN于点O,则下列说法中不一定正确的是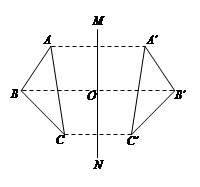
| A.AC=A'C' |
| B.AB∥B'C' |
| C.AA'⊥MN |
| D.BO=B'O |
 (2013•玄武区一模)如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法中不一定正确的是( )
(2013•玄武区一模)如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法中不一定正确的是( )
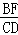 的值(用含α的式子表示出来)
的值(用含α的式子表示出来)