题目内容
【题目】如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形的是( )
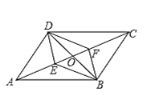
A. AE=CFB. DE=BF
C. ∠ADE=∠CBFD. ∠ABE=∠CDF
【答案】B
【解析】
若是四边形的对角线互相平分,可证明这个四边形是平行四边形,选项A,C,D都能证明对角线互相平分,只有B不可以,由此即可得答案.
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,AD//BC,AB//CD, AD=BC,AB=CD,
∴∠DAE=∠BCF,∠BAE=∠DCF,
A、∵AE=CF,
∴EO=FO,
∵DO=BO,
∴四边形DEBF是平行四边形;
C、∵∠ADE=∠CBF,AD=BC,∠DAE=∠BCF,
∴△ADE≌△CBF,
∴AE=CF,
∴EO=FO,
∵DO=BO,
∴四边形DEBF是平行四边形.
同理若∠ABE=∠CDF,也能证明△ABE≌△CDF,从而四边形DEBF是平行四边形;
只有B选项不能得出结论,
故选B.

练习册系列答案
相关题目
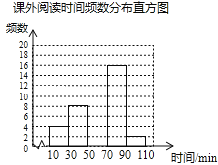
【题目】某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如下不完整的统计表.
课外阅读时间t | 频数 | 百分比 |
10≤t<30 | 4 | 8% |
30≤t<50 | 8 | 16% |
50≤t<70 | a | 40% |
70≤t<90 | 16 | b |
90≤t<110 | 2 | 4% |
合计 | 50 | 100% |
请根据图表中提供的信息回答下列问题:
(1)a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若全校有900名学生,估计该校有多少学生平均每天的课外阅读时间不少于50min?