Question

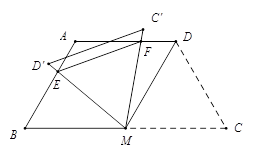
如图，等腰梯形ABCD中，AD∥BC，AD＝AB＝CD＝2，∠C＝60°，M是BC的中点．

（1）求证：△MDC是等边三角形；
（2）将△MDC绕点M旋转，当MD(即MD′)与AB交于一点E，MC(即MC′)同时与AD交于一点F时，点E，F和点A构成△AEF．试探究△AEF的周长是否存在最小值．如果不存在，请说明理由；如果存在，请计算出△AEF周长的最小值．

Answer 1

（1）证明：过点D作DP⊥BC，于点P，过点A作AQ⊥BC于点Q，

∵∠C＝∠B＝60°
∴CP＝BQ＝AB，CP＋BQ＝AB，
又∵ADPQ是矩形，AD＝PQ，
故BC＝2AD，
由已知，点M是BC的中点，
BM＝CM＝AD＝AB＝CD，
即△MDC中，CM＝CD，∠C＝60°，
故△MDC是等边三角形．
（2）解：△AEF的周长存在最小值，理由如下：
连接AM，由（1）平行四边形ABMD是菱形，
△MAB，△MAD和△MC′D′是等边三角形，
∠BMA＝∠BME＋∠AME＝60°，∠EMF＝∠AMF＋∠AME＝60°，
∴∠BME＝∠AMF，
在△BME与△AMF中，BM＝AM，∠EBM＝∠FAM＝60°，
∴△BME≌△AMF(ASA)，
∴BE＝AF，ME＝MF，AE＋AF＝AE＋BE＝AB，
∵∠EMF＝∠DMC＝60°，故△EMF是等边三角形，EF＝MF，
∵MF的最小值为点M到AD的距离，即EF的最小值是，
△AEF的周长＝AE＋AF＋EF＝AB＋EF，
△AEF的周长的最小值为2＋，
所以存在，△AEF的周长的最小值为2＋．

此题考核等边三角形的判定，旋转的性质