题目内容
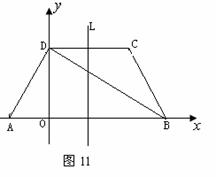
如图11所示,在梯形ABCD中,已知AB∥CD, AD⊥DB,AD=DC=CB,AB=4.以AB所在直线为![]() 轴,过D且垂直于AB的直线为
轴,过D且垂直于AB的直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求∠DAB的度数及A、D、C三点的坐标;
(2)求过A、D、C三点的抛物线的解析式及其对称轴L.
(3)若P是抛物线的对称轴L上的点,那么使![]() PDB为等腰三角形的点P有几个?(不必求点P的坐标,只需说明理由)
PDB为等腰三角形的点P有几个?(不必求点P的坐标,只需说明理由)
解: (1) ![]() DC∥AB,AD=DC=CB,
DC∥AB,AD=DC=CB,
![]() ∠CDB=∠CBD=∠DBA,··············································································· 0.5分
∠CDB=∠CBD=∠DBA,··············································································· 0.5分
 ∠DAB=∠CBA,
∠DAB=∠CBA, ![]() ∠DAB=2∠DBA, ············ 1分
∠DAB=2∠DBA, ············ 1分
∠DAB+∠DBA=90![]() ,
, ![]() ∠DAB=60
∠DAB=60![]() , ·········· 1.5分
, ·········· 1.5分
∠DBA=30![]() ,
,![]() AB=4,
AB=4, ![]() DC=AD=2, ········· 2分
DC=AD=2, ········· 2分
Rt![]() AOD,OA=1,OD=
AOD,OA=1,OD=![]() ,··························· 2.5分
,··························· 2.5分
![]() A(-1,0),D(0,
A(-1,0),D(0, ![]() ),C(2,
),C(2, ![]() ). · 4分
). · 4分
(2)根据抛物线和等腰梯形的对称性知,满足条件的抛物线必过点A(-1,0),B(3,0),
故可设所求为 ![]() =
=![]() (
(![]() +1)(
+1)( ![]() -3) ······························································ 6分
-3) ······························································ 6分
将点D(0, ![]() )的坐标代入上式得,
)的坐标代入上式得, ![]() =
=![]() .
.
所求抛物线的解析式为 ![]() =
=![]() ·········································· 7分
·········································· 7分
其对称轴L为直线![]() =1.······················································································ 8分
=1.······················································································ 8分
(3) ![]() PDB为等腰三角形,有以下三种情况:
PDB为等腰三角形,有以下三种情况:
①因直线L与DB不平行,DB的垂直平分线与L仅有一个交点P1,P1D=P1B,
![]() P1DB为等腰三角形; ················································································· 9分
P1DB为等腰三角形; ················································································· 9分
②因为以D为圆心,DB为半径的圆与直线L有两个交点P2、P3,DB=DP2,DB=DP3, ![]() P2DB,
P2DB, ![]() P3DB为等腰三角形;
P3DB为等腰三角形;
③与②同理,L上也有两个点P4、P5,使得 BD=BP4,BD=BP5. ···················· 10分
由于以上各点互不重合,所以在直线L上,使![]() PDB为等腰三角形的点P有5个.
PDB为等腰三角形的点P有5个.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案

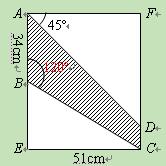
 根据图中的数据帮丁丁计算出BE、CD的长度(精确到个位,
根据图中的数据帮丁丁计算出BE、CD的长度(精确到个位, ≈1.7).
≈1.7).