题目内容
如图所示,半径为2 的⊙O内有互相垂直的两条弦AB、CD相 交于P点。
的⊙O内有互相垂直的两条弦AB、CD相 交于P点。
(1)求证:PA·PB=PC·PD;
(2)设BC中点为F,连结FP并延长交AD于E,求证:EF⊥AD;
(3)若AB=8,CD=6,求OP的长。
 的⊙O内有互相垂直的两条弦AB、CD相 交于P点。
的⊙O内有互相垂直的两条弦AB、CD相 交于P点。(1)求证:PA·PB=PC·PD;
(2)设BC中点为F,连结FP并延长交AD于E,求证:EF⊥AD;
(3)若AB=8,CD=6,求OP的长。

解:(1) ∵∠A、∠C所对的圆弧相同,
∴∠A=∠C,
∴Rt△APD∽Rt△CPB,
∴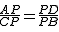 ,
,
∴PA·PB=PC·PD;
(2)∵F为BC的中点,△BPC为Rt△,
∴FP=FC,
∴∠C=∠CPF,
又∠C=∠A,∠DPE=∠CPF,
∴∠A=∠DPE,
∵∠A+∠D=90°,
∴∠DPE+∠D=90°,
∴EF⊥AD;
(3)作OM⊥AB于M,ON⊥CD于N, 由垂径定理,
∴OM2=(2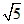 )2-42=4,ON2=(2
)2-42=4,ON2=(2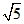 )2-32=11,
)2-32=11,
又易证四边形MONP是矩形MONP矩形,
∴OP=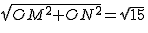 。
。
∴∠A=∠C,
∴Rt△APD∽Rt△CPB,
∴
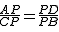 ,
, ∴PA·PB=PC·PD;
(2)∵F为BC的中点,△BPC为Rt△,
∴FP=FC,
∴∠C=∠CPF,
又∠C=∠A,∠DPE=∠CPF,
∴∠A=∠DPE,
∵∠A+∠D=90°,
∴∠DPE+∠D=90°,
∴EF⊥AD;
(3)作OM⊥AB于M,ON⊥CD于N, 由垂径定理,
∴OM2=(2
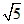 )2-42=4,ON2=(2
)2-42=4,ON2=(2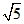 )2-32=11,
)2-32=11,又易证四边形MONP是矩形MONP矩形,
∴OP=
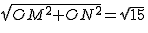 。
。 
练习册系列答案
相关题目

 如图所示,半径为5的⊙O在平面直角坐标系中,横、纵坐标均为整数的点成为整点,横、纵坐标和为零的整点为好整点
如图所示,半径为5的⊙O在平面直角坐标系中,横、纵坐标均为整数的点成为整点,横、纵坐标和为零的整点为好整点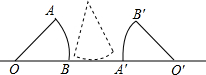 如图所示,半径为1的圆心角为45°的扇形纸片OAB在直线L上向右做无滑动的滚动.且滚动至扇形O′A′B′处,则顶点O所经过的路线总长是
如图所示,半径为1的圆心角为45°的扇形纸片OAB在直线L上向右做无滑动的滚动.且滚动至扇形O′A′B′处,则顶点O所经过的路线总长是 B.
B. C.
C. 8 D.
8 D.

 B.
B. C.
C. 8
D.
8
D.