题目内容
半径为5cm的圆中,有一条长为6cm的弦,则圆心到此弦的距离为
- A.3cm
- B.4cm
- C.5cm
- D.6cm
B
分析:过O向AB作垂线,根据垂径定理和勾股定理求解.
解答: 解:过O向AB作垂线,
解:过O向AB作垂线,
由垂径定理可得AC=BC= AB=
AB= ×6=3cm.
×6=3cm.
在Rt△OBC中,BC=3cm,OB=5cm,
由勾股定理得OC2=OB2-BC2,OC= =
=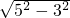 =4cm.
=4cm.
故选B.
点评:本题考查垂径定理的应用.解此类问题一般要把半径、弦心距、弦的一半构建在一个直角三角形里,运用勾股定理求解.
分析:过O向AB作垂线,根据垂径定理和勾股定理求解.
解答:
 解:过O向AB作垂线,
解:过O向AB作垂线,由垂径定理可得AC=BC=
 AB=
AB= ×6=3cm.
×6=3cm.在Rt△OBC中,BC=3cm,OB=5cm,
由勾股定理得OC2=OB2-BC2,OC=
 =
=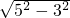 =4cm.
=4cm.故选B.
点评:本题考查垂径定理的应用.解此类问题一般要把半径、弦心距、弦的一半构建在一个直角三角形里,运用勾股定理求解.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
半径为5cm的圆中,有一条长为6cm的弦,则圆心到此弦的距离为( )
| A、3cm | B、4cm | C、5cm | D、6cm |