Question

在半径为5cm的圆中，弦AB∥CD，AB=6cm，CD=8cm，则弦AB与CD之间的距离是

 

．

Answer 1

分析：先根据题意画出图形，注意圆心与两弦的位置关系有两种情况：同旁或两旁．所以本题的答案有两个．

解答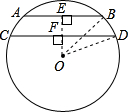：解：过点O作OE⊥AB于E
∵AB∥CD，∴OF⊥CD
∵OE过圆心，OE⊥AB
∴EB=

1

2

AB=3cm
∵OB=5cm，∴EO=4cm
同理，OF=3cm
∴EF=1cm
当AB、CD位于圆心两旁时EF=7cm
∴EF=1cm或EF=7cm．

点评：本题利用了垂径定理和勾股定理求解，注意要分两种情况讨论．