Question

【题目】抛物线y=x2+bx+c与x轴交于A(5,0)、B(-1,0)两点，过点A作直线AC⊥x轴，交直线y=2x于点C.

（1）求该抛物线的解析式；

（2）求点A关于直线y=2x的对称点A′的坐标，判定点A′是否在抛物线上，并说明理由；

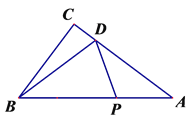
（3）点P是抛物线上一动点，过点P作y轴的平行线，交线段CA′于点M，是否存在这样的点P，使四边形PACM是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由.

Answer 1

【答案】（1）．（2）点A/的坐标为（﹣3,4）．点A/在该抛物线上．（3）点P运动到时，四边形PACM是平行四边形．

【解析】试题分析：（1）利用待定系数法求出抛物线的解析式；

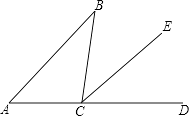
（2）首先求出对称点A′的坐标，然后代入抛物线解析式，即可判定点A′是否在抛物线上．本问关键在于求出A′的坐标．如答图所示，作辅助线，构造一对相似三角形Rt△A′EA∽Rt△OAC，利用相似关系、对称性质、勾股定理，求出对称点A′的坐标；

（3）本问为存在型问题．解题要点是利用平行四边形的定义，列出代数关系式求解．如答图所示，平行四边形的对边平行且相等，因此PM=AC=10；利用含未知数的代数式表示出PM的长度，然后列方程求解．

试题解析：（1）∵与x轴交于A（5,0）、B（-1,0）两点，

∴，

解得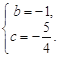

∴抛物线的解析式为．

（2） 过点作⊥x轴于E，AA/与OC交于点D，

∵点C在直线y=2x上，

∴C（5，10）

∵点A和关于直线y=2x对称，∴OC⊥，=AD．

∵OA=5，AC=10,∴．

∵,

∴．

∴．

在和中，

∵∠+∠=90°，∠ACD+∠=90°，

∴∠=∠ACD．

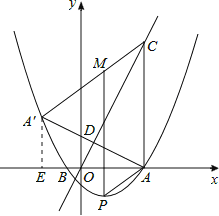
又∵∠=∠OAC=90°，

∴∽．

∴即．

∴=4，AE=8．

∴OE=AE－OA=3．

∴点A/的坐标为（﹣3,4）．

当x=﹣3时， ．

所以，点A/在该抛物线上．

（3）存在．

理由：设直线的解析式为y=kx+b,

则，

解得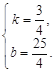

∴直线的解析式为．

设点P的坐标为，则点M为．

∵PM∥AC，

∴要使四边形PACM是平行四边形,只需PM=AC．又点M在点P的上方，

∴．

解得（不合题意,舍去）当x=2时，．

∴当点P运动到时，四边形PACM是平行四边形．