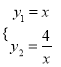题目内容
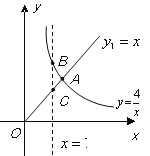
【题目】如图,函数y=![]() 和y= - x+4的图像交点为A、B,原点为O,求△AOB面积.
和y= - x+4的图像交点为A、B,原点为O,求△AOB面积.

【答案】8![]()
【解析】整体分析:
联立方程y=![]() 和y= - x+4,求出点A,B的坐标,然后由公式△OAB的面积=
和y= - x+4,求出点A,B的坐标,然后由公式△OAB的面积=![]() ×(x1- x2)(y2- y1)求解.
×(x1- x2)(y2- y1)求解.
解:把y=![]() 代入y= - x+4得,
代入y= - x+4得,
![]() = - x+4,
= - x+4,
解得x1=2+![]() ,x2=2-
,x2=2-![]() .
.
所以y1=2-![]() ,y2=2+
,y2=2+![]() .
.
则A(2-![]() ,2+
,2+![]() ),B(2+
),B(2+![]() ,2-
,2-![]() ),
),
所以△OAB的面积=![]() ×(x1- x2)(y2- y1)==
×(x1- x2)(y2- y1)==![]() ×4
×4![]() ×4
×4![]() =
=![]() .
.
【题型】解答题
【结束】
19
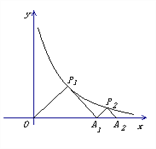
【题目】如图,直线![]() 与双曲线
与双曲线![]() 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.

(1)求m及k的值;
(2)不解关于x、y的方程组 直接写出点B的坐标;
直接写出点B的坐标;
(3)直线![]() 经过点B吗?请说明理由.
经过点B吗?请说明理由.
【答案】(1)m=-1,k=2;(2)(-1,-2);(3)经过
【解析】试题分析:(1)把A(2,1)分别代入直线![]() 与双曲线
与双曲线![]() 即可求得结果;
即可求得结果;
(2)根据函数图象的特征写出两个图象的交点坐标即可;
(3)把x=-1,m=-1代入![]() 即可求得y的值,从而作出判断.
即可求得y的值,从而作出判断.
(1)把A(2,1)分别代入直线![]() 与双曲线
与双曲线![]() 的解析式得m=-1,k=2;
的解析式得m=-1,k=2;
(2)由题意得B的坐标(-1,-2);
(3)当x=-1,m=-1代入![]() 得y=-2×(-1)+4×(-1)=2-4=-2
得y=-2×(-1)+4×(-1)=2-4=-2
所以直线![]() 经过点B(-1,-2).
经过点B(-1,-2).

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目