Question

【题目】如图，AO⊥OM，OA=8，点B为射线OM上的一个动点，分别以OB，AB为直角边，B为直角顶点，在OM两侧作等腰Rt△OBF、等腰Rt△ABE，连接EF交OM于P点，当点B在射线OM上移动时，PB的长度为_______.

Answer 1

【答案】4

【解析】

作辅助线，首先证明△ABO≌△BEN，得到BO=ME；进而证明△BPF≌△NPE，即可解决问题．

解：如图，过点E作EN⊥BM，垂足为点N，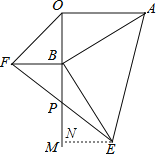

∵∠AOB=∠ABE=∠BNE=90°，
∴∠ABO+∠BAO=∠ABO+∠NBE=90°，
∴∠BAO=∠NBE，
∵△ABE、△BFO均为等腰直角三角形，
∴AB=BE，BF=BO；
在△ABO与△BEN中，

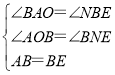
∴△ABO≌△BEN（AAS），
∴BO=NE，BN=AO；
∵BO=BF，
∴BF=NE，
在△BPF与△NPE中，

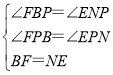
∴△BPF≌△NPE（AAS），
∴BP=NP=BN；而BN=AO，
∴BP=AO=×8=4，
故答案为：4．