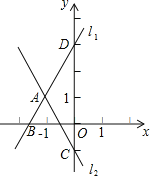题目内容
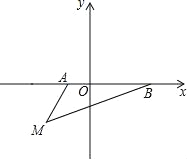
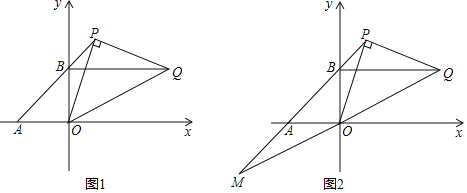
【题目】已知:如图,直线AB交两坐标轴于A(a,0)、B(0,b)两点,且a,b满足等式:![]() +(b﹣4)2=0,点P为直线AB上第一象限内的一动点,过P作OP的垂线且与过B点且平行于x轴的直线相交于点Q,
+(b﹣4)2=0,点P为直线AB上第一象限内的一动点,过P作OP的垂线且与过B点且平行于x轴的直线相交于点Q,
(1)求A,B两点的坐标;
(2)当P点在直线AB上的第一象限内运动时,![]() AP﹣BQ的值变不变?如果不变,请求出这个定值;若变化请说明理由.
AP﹣BQ的值变不变?如果不变,请求出这个定值;若变化请说明理由.
(3)延长QO与直线AB交于点M.请判断出线段AP,BM,PM三条线段构成三角形的形状,说明理由.
【答案】(1) A(﹣4,0)、B(0,4);(2)见解析;(3)见解析.
【解析】
(1)由![]() +(b-4)2直接可求a=-4,b=4;
+(b-4)2直接可求a=-4,b=4;
(2)过点P作PN⊥AP,交x轴于点N,连接QN,则AN=![]() AP,根据角的关系可证QM⊥ON,BQ=ON,
AP,根据角的关系可证QM⊥ON,BQ=ON,![]() AP-BQ=AN-ON=AO=4;
AP-BQ=AN-ON=AO=4;
(3)直线AB的解析式y=x+4,设P(m,4+m),分别求出直线PO的解析式为y=![]() x,直线PQ的解析式y=-
x,直线PQ的解析式y=-![]() x+
x+![]() ,根据Q点纵坐标与B点纵坐标相同,可求Q(2m+4,4),求出OQ的直线解析式为y=
,根据Q点纵坐标与B点纵坐标相同,可求Q(2m+4,4),求出OQ的直线解析式为y=![]() x,M(
x,M(![]() ,
,![]() ),分别将边表示出来PA2=2(m+4)2,BM2=2
),分别将边表示出来PA2=2(m+4)2,BM2=2![]() ,PM2=2
,PM2=2 ,利用勾股定理即可求解;
,利用勾股定理即可求解;
(1)![]() +(b﹣4)2,
+(b﹣4)2,
∴a=﹣4,b=4,
∴A(﹣4,0)、B(0,4);
(2)如图1:过点P作PN⊥AP,交x轴于点N,连接QN,
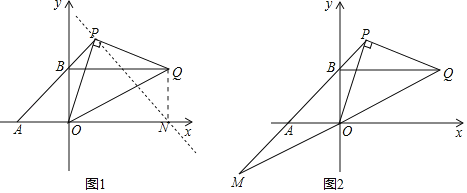
∵AO=BO=4,
∴∠PAN=45°,
∴AN=![]() AP,
AP,
∵∠BOP=∠PQO,
∴∠PQO+∠PON=90°,
∵∠OPQ=90°,
∴∠BQN+∠QNO=180°,
∵BQ∥ON,
∴QM⊥ON,
∴BQ=ON,
∴![]() AP﹣BQ=AN﹣ON=AO=4;
AP﹣BQ=AN﹣ON=AO=4;
(3)直线AB的解析式y=x+4,
设P(m,4+m),
直线PO的解析式为y=![]() x,
x,
∴直线PQ的解析式y=﹣![]() x+
x+![]() ,
,
∵Q点纵坐标为4,
∴4=﹣![]() x+
x+![]() 时,x=2m+2,
时,x=2m+2,
Q(2m+4,4),
∴OQ的直线解析式为y=![]() x,
x,
当![]() x=x+4时,x=
x=x+4时,x=![]() ,
,
∴M(![]() ,
,![]() )
)
∴PA2=2(m+4)2,
BM2=2![]() ,
,
PM2=2 ,
,
∴PA2+BM2=PM2,
∴线段AP,BM,PM三条线段构成三角形直角三角形;

 优学名师名题系列答案
优学名师名题系列答案