��Ŀ����
����Ŀ����3�Ų����Ŀ�Ƭ��������д�в�ͬ�������⣬��������ͬ���������ſ�Ƭ���泯��ϴ�Ⱥ�һ�δ��������ȡһ�ţ��������ſ�Ƭ���е����ּ������κ�������ʽy��a��x��2��2+c�е�a���ڶ��δ����µ����ſ�Ƭ���������ȡһ�ţ�������е����ּ�������ʽ�е�c��
��1������aʹ�����߿������ϵĸ��ʣ�
��2����������y��a��x��2��2+c�Ķ����ڵ������ĸ��ʣ�������״ͼ���б�����⣩
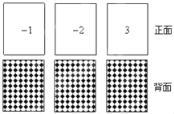
���𰸡���1�����aʹ�����߿������ϵĸ���Ϊ![]() ����2��������y��a��x��2��2+c�Ķ����ڵ������ĸ���Ϊ
����2��������y��a��x��2��2+c�Ķ����ڵ������ĸ���Ϊ![]() ��
��
��������
��1��������������ֻ��һ��3�����aΪ�����ĸ��ʼ��ɣ�
��2�����������б��ó����еȿ��ܵ���������ҳ������������������������������ʣ�
��1��������3���ƣ�ֻ��1����������
�����aʹ�����߿������ϵĸ���Ϊ![]() ��
��
��2������״ͼ���£�
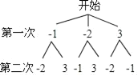
����״ͼ֪�������ߵĶ�������Ϊ��2����2������2��3������2����1������2��3������2����2������2����1����6�ֿ��ܽ����
���У������ڵ���������4�ֽ����
����������y��a��x��2��2+c�Ķ����ڵ������ĸ���Ϊ![]() ��
��