题目内容
如下图，已知AB=BC，D是AB上一点，DE⊥AC于E，ED的延长线交CB的延长线于F。
试探索△BDF的形状，并说明理由。
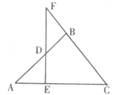
答：△BDF为等腰三角形
证明：∵DE⊥AC于E，∴∠A＋∠ADE=90°，∠C＋∠F=90°
又∵BA=BC，∴∠A＝∠C，∴∠ADE=∠F
又∵∠ADE＝∠BDF，∴∠BDF＝∠F，∴BF＝BD
∴△BDF为等腰三角形．
练习册系列答案
提分百分百检测卷系列答案
相关题目
提分百分百检测卷系列答案题目内容
如下图，已知AB=BC，D是AB上一点，DE⊥AC于E，ED的延长线交CB的延长线于F。
试探索△BDF的形状，并说明理由。
答：△BDF为等腰三角形
证明：∵DE⊥AC于E，∴∠A＋∠ADE=90°，∠C＋∠F=90°
又∵BA=BC，∴∠A＝∠C，∴∠ADE=∠F
又∵∠ADE＝∠BDF，∴∠BDF＝∠F，∴BF＝BD
∴△BDF为等腰三角形．
提分百分百检测卷系列答案
