题目内容
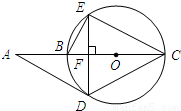
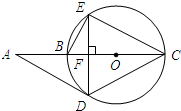
如图,△DEC内接于⊙O,AC经过圆心O交⊙O于点B,且AC⊥DE,垂足为F,连接AD、BE,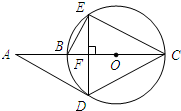 若sinA=
若sinA=| 1 | 2 |
(1)求证:AD是⊙O的切线;
(2)△DCE是否是等边三角形?请说明理由;
(3)若⊙O的半径R=2,试求CE的长.
分析:(1)连接OD.根据题意可求出∠AOD,∠A,从而得出∠ADO=90°,则AD是⊙O的切线;
(2)先得结论△DCE是等边三角形,由题意得CE=CD,再由BC是⊙O的直径,则∠BEC=90°,从而求得∠DEC=60°,则△DCE是等边三角形.
(3)由题意可求得BC,即可得出∠BEC,在Rt△BEC中,由三角函数求出CE的长.
(2)先得结论△DCE是等边三角形,由题意得CE=CD,再由BC是⊙O的直径,则∠BEC=90°,从而求得∠DEC=60°,则△DCE是等边三角形.
(3)由题意可求得BC,即可得出∠BEC,在Rt△BEC中,由三角函数求出CE的长.
解答: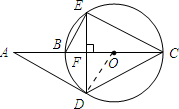 解:(1)连接OD.
解:(1)连接OD.
∵∠BED=30°,∴∠AOD=60°,
∵sinA=
∴∠A=30°
∴∠A+∠AOD=90°
∴∠ADO=90°
∴AD是⊙O的切线.
(2)△DCE是等边三角形.理由如下:
∵BC为⊙O的直径且AC⊥DE.
∴
=
.∴CE=CD.
∵BC是⊙O的直径,∴∠BEC=90°,
∵∠BED=30°,
∴∠DEC=60°,
∴△DCE是等边三角形.
(3)∵⊙O的半径R=2.
∴直径BC=4
∵△DCE是等边三角形,
∴∠EDC=60°
∴∠EBC=60°
在Rt△BEC中,sin∠EBC=
,
∴CE=BCsin60°=4×
=2
.
 解:(1)连接OD.
解:(1)连接OD.∵∠BED=30°,∴∠AOD=60°,
∵sinA=
| 1 |
| 2 |
∴∠A=30°
∴∠A+∠AOD=90°
∴∠ADO=90°
∴AD是⊙O的切线.
(2)△DCE是等边三角形.理由如下:
∵BC为⊙O的直径且AC⊥DE.
∴
 |
| CE |
 |
| CD |
∵BC是⊙O的直径,∴∠BEC=90°,
∵∠BED=30°,
∴∠DEC=60°,
∴△DCE是等边三角形.
(3)∵⊙O的半径R=2.
∴直径BC=4
∵△DCE是等边三角形,
∴∠EDC=60°
∴∠EBC=60°
在Rt△BEC中,sin∠EBC=
| CE |
| BC |
∴CE=BCsin60°=4×
| ||
| 2 |
| 3 |
点评:本题考查了切线的判定、等边三角形的判定和性质、圆周角定理以及解直角三角形.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
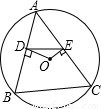
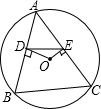 如图,△ABC内接于⊙O,OD⊥AB于D,OE⊥AC于E,⊙O的半径为1,则sinA的值等于线段( )的长.
如图,△ABC内接于⊙O,OD⊥AB于D,OE⊥AC于E,⊙O的半径为1,则sinA的值等于线段( )的长.| A、AD | B、DE | C、AE | D、OD |
 若
若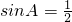 ,∠BED=30°.
,∠BED=30°.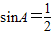 ,∠BED=30°.
,∠BED=30°.