题目内容
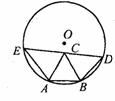
 如图,已知AB是半径为1的圆O的一条弦,且AB<1,以AB为一边在圆O内作正△ABC,点D为圆O上不同于点A的一点,且DB=AB,DC的延长线交圆O于点E,试探究AE的长是否为定值(不随AB长度的变化而变化)?若为定值,求出这个定值;若不为定值,试确定AE与AB长之间的关系.________.
如图,已知AB是半径为1的圆O的一条弦,且AB<1,以AB为一边在圆O内作正△ABC,点D为圆O上不同于点A的一点,且DB=AB,DC的延长线交圆O于点E,试探究AE的长是否为定值(不随AB长度的变化而变化)?若为定值,求出这个定值;若不为定值,试确定AE与AB长之间的关系.________.
AE=OA
分析:根据四点共圆的性质得到四边形的对角互补,然后根据等边三角形的内角的度数进一步得到△EAC与△OAB全等进而确定两对应线段的关系.
解答:由A、B、D、E四点共圆,
∴∠EAB+∠EDB=180°,
∵BC=BD,∠BDC=∠BCD,∠BCD+∠ECB=180°,
∴∠ECB=∠EAB
又∵∠CAB=∠ACB=60°
∴∠ECB-∠ACB=∠EAB-∠CAB,
∴∠ECA=∠EAC,
∴△EAC是等腰三角形,
∵AB=BD,
∴∠OEA=∠DOB,
∵AC=AB,
∴△EAC≌△OAB,
∴AE=OA.
点评:本题考查了四点共圆、三角形全等的判定及圆心角圆周角之间的关系,解题的关键是利用四点共圆的性质及等腰三角形的性质得到全等三角形,进而确定两线段的关系.
分析:根据四点共圆的性质得到四边形的对角互补,然后根据等边三角形的内角的度数进一步得到△EAC与△OAB全等进而确定两对应线段的关系.
解答:由A、B、D、E四点共圆,
∴∠EAB+∠EDB=180°,
∵BC=BD,∠BDC=∠BCD,∠BCD+∠ECB=180°,
∴∠ECB=∠EAB
又∵∠CAB=∠ACB=60°
∴∠ECB-∠ACB=∠EAB-∠CAB,
∴∠ECA=∠EAC,
∴△EAC是等腰三角形,
∵AB=BD,
∴∠OEA=∠DOB,
∵AC=AB,
∴△EAC≌△OAB,
∴AE=OA.
点评:本题考查了四点共圆、三角形全等的判定及圆心角圆周角之间的关系,解题的关键是利用四点共圆的性质及等腰三角形的性质得到全等三角形,进而确定两线段的关系.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 14、如图,已知AB是半径为1的圆O的一条弦,且AB<1,以AB为一边在圆O内作正△ABC,点D为圆O上不同于点A的一点,且DB=AB,DC的延长线交圆O于点E,试探究AE的长是否为定值(不随AB长度的变化而变化)?若为定值,求出这个定值;若不为定值,试确定AE与AB长之间的关系.
14、如图,已知AB是半径为1的圆O的一条弦,且AB<1,以AB为一边在圆O内作正△ABC,点D为圆O上不同于点A的一点,且DB=AB,DC的延长线交圆O于点E,试探究AE的长是否为定值(不随AB长度的变化而变化)?若为定值,求出这个定值;若不为定值,试确定AE与AB长之间的关系.
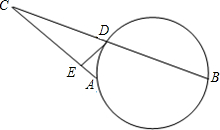 如图,已知AB是⊙O的直径,⊙O过BC的中点D,且ED是⊙O的切线.
如图,已知AB是⊙O的直径,⊙O过BC的中点D,且ED是⊙O的切线.