题目内容
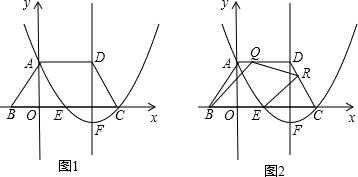
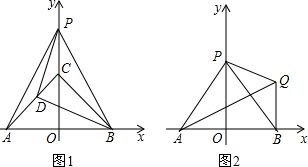
已知,如图1,在直角坐标系中,有等腰梯形ABCD,AD∥BC,AB=CD,抛物线 交x轴于点E、C(点C在点E的右侧),交y轴于点A,它的对称轴过点D,顶点为点F;
交x轴于点E、C(点C在点E的右侧),交y轴于点A,它的对称轴过点D,顶点为点F;(1)求点A、B、C、D的坐标;
(2)点P是抛物线在第一象限内的点,它到边AB、BC所在直线的距离相等,求出点P的坐标;
(3)如图2,若点Q是线段AD上的一个动点,AQ=t,以BQ为一边作∠BQR=120°,交CD于点R,连接ER、FC,试探究:是否存在t的值,使ER∥FC?若存在,求出t的值;若不存在,请说明理由.

【答案】分析:(1)抛物线解析式中,令y=0,能求得点E、C的坐标;令x=0,能求得点A的坐标;若设抛物线对称轴与x轴的交点为G,根据E、C的坐标即可得到点G的坐标,结合点A的坐标可得到点D的坐标;根据等腰梯形的性质可知OB=CG,可据此求出点B的坐标.
(2)在Rt△ABO中,易求得∠ABO=60°,作∠ABO的角平分线,交y轴于点H,那么显然∠HBO=30°,OB长已知,通过解直角三角形不难得到点H的坐标,利用待定系数法可求出直线BH的解析式,联立直线BH和抛物线的解析式即可得到点P的坐标.
(3)易知∠BAD=∠ADC=120°,而∠BQR=120°,那么∠ABQ+∠BQA=∠DQR+∠BQA=180°-∠BQR=60°,根据这个条件不难判断出△BAQ和△QDR是相似的,由此得到的条件是 BA:QD=AQ:DR,在这个比例关系式中,AB的长易知,AQ、QD的长都可由t表示出来,关键是求出DR的长,那么就要从BR∥FC的条件入手;点F的坐标易得,首先根据点F、C的坐标判断出∠FCE=∠REC=30°,那么显然△ERC是一个含30°角的特殊直角三角形,EC的长已知,则RC的长可得,而DR=CD-RC,则条件备齐.
解答:解:(1)抛物线y=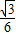 (x-2)(x-6)中,令y=0,得 x1=2、x2=6;
(x-2)(x-6)中,令y=0,得 x1=2、x2=6;
令x=0,得:y=2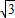 ;
;
∴A(0,2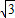 )、E(2,0)、C(6,0);
)、E(2,0)、C(6,0);
设抛物线的对称轴与x轴的交点为G,根据抛物线的对称性知G(4,0),则D(4,2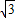 );
);
在等腰梯形ABCD中,OB=CG=2,则 B(-2,0).
 (2)在Rt△ABO中,OA=2
(2)在Rt△ABO中,OA=2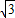 ,OB=2,那么 tan∠ABO=
,OB=2,那么 tan∠ABO=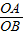 =
=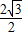 =
=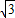 ,∠ABO=60°;
,∠ABO=60°;
作直线BH,使得∠HBO= ∠ABO=30°,交y轴于点H,则H(0,
∠ABO=30°,交y轴于点H,则H(0,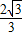 ),
),
∴直线BH:y= x+
x+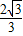 ;
;
由于点P到直线AB、BC的距离相等,所以点P在∠ABO的角平分线上,即点P为直线BH与抛物线的交点;
联立直线BH与抛物线的解析式,有:
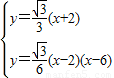 ,解得
,解得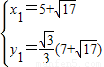 ,
,
∴P点的坐标为(5+ ,
,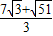 )、(5-
)、(5-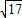 ,
,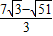 ).
).
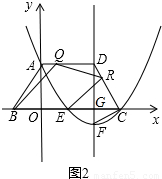 (3)由(1)的抛物线解析式可得:F(4,-
(3)由(1)的抛物线解析式可得:F(4,-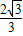 );
);
在Rt△FCG中,FG= ,CG=2,所以tan∠FCG=
,CG=2,所以tan∠FCG=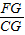 =
=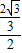 =
= ,即∠FCG=30°;
,即∠FCG=30°;
∵FC∥ER,∴∠REC=∠FCG=30°;
由(1)知,∠ABO=∠DCO=60°,∴∠ERC=90°;
在Rt△ERC中,EC=4,∠REC=30°,则 CR= EC=2,DR=CD-CR=4-2=2;
EC=2,DR=CD-CR=4-2=2;
∵∠BAQ=∠BQR=120°,
∴∠ABQ=∠DQR=60°-∠DQR,又∠BAQ=∠QDR,
∴△BAQ∽△QDR,则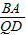 =
=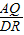
∴ =
= ,化简,得:t2-4t+8=0
,化简,得:t2-4t+8=0
△=(-4)2-4×8<0,因此不存在符合条件的t值.
点评:此题是函数与几何的综合题,主要涉及了函数图象交点坐标的求法、抛物线的对称性、等腰梯形的性质、三角形内角和定理、平行线的性质、角平分线的性质、相似三角形的判定和性质等等重要知识点,综合性较强.最后一题中,通过各角的度数判断出与题相关的相似三角形是解题的关键所在,也是此题的难点所在.
(2)在Rt△ABO中,易求得∠ABO=60°,作∠ABO的角平分线,交y轴于点H,那么显然∠HBO=30°,OB长已知,通过解直角三角形不难得到点H的坐标,利用待定系数法可求出直线BH的解析式,联立直线BH和抛物线的解析式即可得到点P的坐标.
(3)易知∠BAD=∠ADC=120°,而∠BQR=120°,那么∠ABQ+∠BQA=∠DQR+∠BQA=180°-∠BQR=60°,根据这个条件不难判断出△BAQ和△QDR是相似的,由此得到的条件是 BA:QD=AQ:DR,在这个比例关系式中,AB的长易知,AQ、QD的长都可由t表示出来,关键是求出DR的长,那么就要从BR∥FC的条件入手;点F的坐标易得,首先根据点F、C的坐标判断出∠FCE=∠REC=30°,那么显然△ERC是一个含30°角的特殊直角三角形,EC的长已知,则RC的长可得,而DR=CD-RC,则条件备齐.
解答:解:(1)抛物线y=
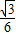 (x-2)(x-6)中,令y=0,得 x1=2、x2=6;
(x-2)(x-6)中,令y=0,得 x1=2、x2=6;令x=0,得:y=2
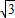 ;
;∴A(0,2
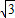 )、E(2,0)、C(6,0);
)、E(2,0)、C(6,0);设抛物线的对称轴与x轴的交点为G,根据抛物线的对称性知G(4,0),则D(4,2
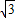 );
);在等腰梯形ABCD中,OB=CG=2,则 B(-2,0).
 (2)在Rt△ABO中,OA=2
(2)在Rt△ABO中,OA=2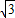 ,OB=2,那么 tan∠ABO=
,OB=2,那么 tan∠ABO=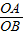 =
=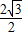 =
=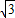 ,∠ABO=60°;
,∠ABO=60°;作直线BH,使得∠HBO=
 ∠ABO=30°,交y轴于点H,则H(0,
∠ABO=30°,交y轴于点H,则H(0,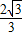 ),
),∴直线BH:y=
 x+
x+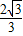 ;
;由于点P到直线AB、BC的距离相等,所以点P在∠ABO的角平分线上,即点P为直线BH与抛物线的交点;
联立直线BH与抛物线的解析式,有:
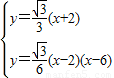 ,解得
,解得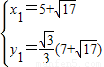 ,
,
∴P点的坐标为(5+
 ,
,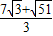 )、(5-
)、(5-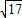 ,
,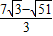 ).
). (3)由(1)的抛物线解析式可得:F(4,-
(3)由(1)的抛物线解析式可得:F(4,-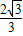 );
);在Rt△FCG中,FG=
 ,CG=2,所以tan∠FCG=
,CG=2,所以tan∠FCG=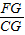 =
=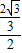 =
= ,即∠FCG=30°;
,即∠FCG=30°;∵FC∥ER,∴∠REC=∠FCG=30°;
由(1)知,∠ABO=∠DCO=60°,∴∠ERC=90°;
在Rt△ERC中,EC=4,∠REC=30°,则 CR=
 EC=2,DR=CD-CR=4-2=2;
EC=2,DR=CD-CR=4-2=2;∵∠BAQ=∠BQR=120°,
∴∠ABQ=∠DQR=60°-∠DQR,又∠BAQ=∠QDR,
∴△BAQ∽△QDR,则
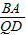 =
=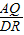
∴
 =
= ,化简,得:t2-4t+8=0
,化简,得:t2-4t+8=0△=(-4)2-4×8<0,因此不存在符合条件的t值.
点评:此题是函数与几何的综合题,主要涉及了函数图象交点坐标的求法、抛物线的对称性、等腰梯形的性质、三角形内角和定理、平行线的性质、角平分线的性质、相似三角形的判定和性质等等重要知识点,综合性较强.最后一题中,通过各角的度数判断出与题相关的相似三角形是解题的关键所在,也是此题的难点所在.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
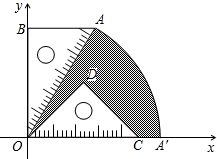 ODC的斜边OC的长相等,把这两块三角板放置在如图所示的平面直角坐标系中,且AB=3,AO=6.
ODC的斜边OC的长相等,把这两块三角板放置在如图所示的平面直角坐标系中,且AB=3,AO=6.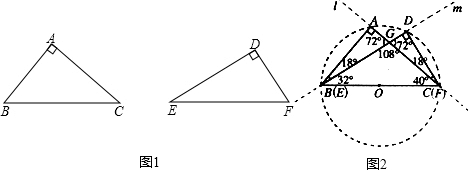
 D为AC的中点.
D为AC的中点.