题目内容
【题目】如图，△ABC与△CDE都是等边三角形，点E、F分别为AC、BC的中点。
（1） 求证：四边形EFCD是菱形；（2）如果AB=10，求D、F两点间的距离。
【答案】（1）证明见解析（2）
【解析】
试题分析：（1）利用三角形的中位线定理即可得到四边形EFCD的四边相等，即可证得；
（2）连接DF，与EC相交于点G，△EFC是等边三角形，则△EFG是直角三角形，利用三角函数即可求得GF的长，根据DF=2GF即可求得．
试题解析：（1）∵△ABC与△CDE都是等边三角形
∴ AB=AC=BC，ED=DC=EC
∵ 点E、F分别为AC、BC的中点
∴EF= 
，EC= 
, FC=
∴EF=EC=FC
∴EF=FC=ED=DC，
∴四边形EFCD是菱形．
（2）连接DF，与EC相交于点G，
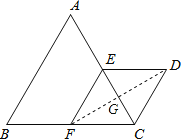
∵四边形EFCD是菱形
∴DF⊥EC，FD=2FG
∵EF= =5, EG=
EC=
,
由勾股定理得：FG=
，则FD=
练习册系列答案
相关题目