Question

【题目】已知：△ABC中，AB=AC，∠B=α．
（1）如图1，点D，E分别在边AB，AC上，线段DE的垂直平分线MN交直线BC于点M，交DE于点N，求证：BD+CE=BC．需补充条件∠EMN= （用含α的式子表示）补充条件后并证明；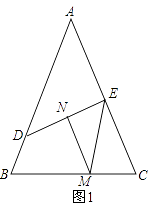

（2）把（1）中的条件改为点D，E分别在边BA、AC延长线上，线段DE的垂直平分线MN交直线BC于点M，交DE于点N（如图2），并补充条件∠EMN=（用含α的式子表示），通过观察或测量，猜想线段BD，CE与BC之间满足的数量关系，并予以证明．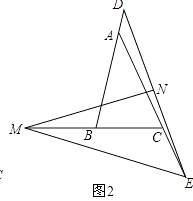

Answer 1

【答案】
（1）解：当∠EMN= α时，BD+CE=BC．
理由：如图1所示：连接DM．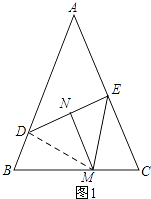

∵AB=AC，
∴∠B=∠C=α．
∵MN是DE的垂直平分线，
∴DN=NE，DM=EM．
在△MND和△MNE中，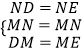
，
∴△MND≌△MNE．
∴∠DMN=∠EMN= α．
∴∠DME=α．
∵∠C+∠CEM=∠DMB+∠DME，∠C=∠DME=α，
∴∠DMB=∠CEM．
在△BDM和△CME中，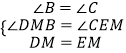
，
∴△BDM≌△CME．
∴BD=MC，EC=BM．
又∵MB+MC=BC，
∴BD+EC=BC．
（2）解：当∠EMN= α时，BD=CE+BC．

∵AB=AC，
∴∠ABC=∠ACB．
∴∠DBM=∠MCE．
∵MN是DE的垂直平分线，
∴DN=NE，DM=EM．
在△MND和△MNE中，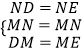
，
∴△MND≌△MNE．
∴∠DMN=∠EMN= α．
∴∠EMD=∠B=α
∵∠BMD+∠MDB=α，∠EMC+∠CMD=α，
∴∠EMC=∠MDB．
在△BDM和△CME中，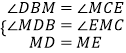
，
∴△BDM≌△CME．
∴BD=MC，EC=BM．
又∵MB+BC=MC，
∴EC+BC=BD
【解析】（1）当∠EMN= α时，BD+CE=BC．连接DM．先证明∠DME=α．接下来证明∠DMB=∠CEM．然后依据AAS可证明△BDM≌△CME，然后由全等三角形的性质可证得BD=MC，EC=BM，结合条件MB+MC=BC，可证得问题的结论；（2）当∠EMN= α时，BD=CE+BC．先证明∠DMN=∠EMN= α．从而得到∠EMD=∠B=α，接下来，依据等角的补角相等可证得∠DBM=∠MCE，然后依据三角形的外角的性质和角的和差关系证明∠MDB=∠EMC，然后依据AAS可证明△BDM≌△CME，由全等三角形的性质可得到BD=MC，EC=BM，结合MB+BC=MC可证得EC+BC=BD．
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识，掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等．