题目内容
 请把下列证明过程补充完整:
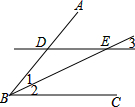
请把下列证明过程补充完整:已知:如图,DE∥BC,BE平分∠ABC.求证:△DBE为等腰三角形.
证明:因为BE平分∠ABC(已知),
所以∠1=∠2(角平分线性质).
又因为DE∥BC(已知),
所以∠DEB=
所以∠1=
所以△DBE为等腰三角形
考点:等腰三角形的判定
专题:推理填空题
分析:根据平行线性质和角平分线定义得出∠1=∠2=∠DEB,即可得出△DBE为等腰三角形.
解答:证明:因为BE平分∠ABC(已知),
所以∠1=∠2(角平分线性质).
又因为DE∥BC(已知),
所以∠DEB=∠2.
所以∠1=∠DEB.
所以△DBE为等腰三角形(等角对等边).
故答案为:∠2,∠DEB,(等角对等边).
所以∠1=∠2(角平分线性质).
又因为DE∥BC(已知),
所以∠DEB=∠2.
所以∠1=∠DEB.
所以△DBE为等腰三角形(等角对等边).
故答案为:∠2,∠DEB,(等角对等边).
点评:本题考查了等腰三角形的判定、角平分线定义,平行线性质等知识点的应用,主要考查学生的推理能力.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
在0.2,-(-5),-|-2
|,15%,0,5×(-1)3,-22,-(-2)2这八个数中,非负数有( )
| 1 |
| 2 |
| A、4个 | B、5个 | C、6个 | D、7个 |
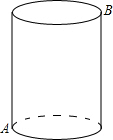 如图,圆柱的底圆面积是
如图,圆柱的底圆面积是 如图,在四边形ABCD中,AB>CD,E、F分别是对角线BD、AC的中点,求证:EF>
如图,在四边形ABCD中,AB>CD,E、F分别是对角线BD、AC的中点,求证:EF>