题目内容
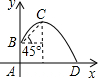 如图,AB是自动喷灌设备的水管,点A在地面,点B高出地面1.5米.在B处有一自动旋转的喷水头,在每一瞬间,喷出的水流呈抛物线状,喷头B与水流最高点C的连线与水平线成45°角,水流的最高点C与喷头B高出2米,在如图的坐标系中,水流的落地点D到点A的距离是
如图,AB是自动喷灌设备的水管,点A在地面,点B高出地面1.5米.在B处有一自动旋转的喷水头,在每一瞬间,喷出的水流呈抛物线状,喷头B与水流最高点C的连线与水平线成45°角,水流的最高点C与喷头B高出2米,在如图的坐标系中,水流的落地点D到点A的距离是分析:根据所建坐标系,易知B点坐标和顶点C的坐标,设抛物线解析式为顶点式,可求表达式,求AD长就是求y=0是x的值.
解答: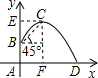 解:如图,建立直角坐标系,过C点作CE⊥y轴于E,过C点作CF⊥x轴于F,
解:如图,建立直角坐标系,过C点作CE⊥y轴于E,过C点作CF⊥x轴于F,
∴B(0,1.5),
∴∠CBE=45°,
∴EC=EB=2米,
∵CF=AB+BE=2+1.5=3.5,
∴C(2,3.5)
设抛物线解析式为:y=a(x-2)2+3.5,
又∵抛物线过点B,
∴1.5=a(0-2)2+3.5
∴a=-
,
∴y=-
(x-2)2+3.5=-
x2+2x+
,
∴所求抛物线解析式为:y=-
x2+2x+
,
∵抛物线与x轴相交时,y=0,
∴0=-
x2+2x+
,
∴x1=2+
,x2=2-
(舍去)
∴D( 2+
,0)
∴水流落点D到A点的距离为:2+
米.
故答案为:2+
.
 解:如图,建立直角坐标系,过C点作CE⊥y轴于E,过C点作CF⊥x轴于F,
解:如图,建立直角坐标系,过C点作CE⊥y轴于E,过C点作CF⊥x轴于F,∴B(0,1.5),
∴∠CBE=45°,
∴EC=EB=2米,
∵CF=AB+BE=2+1.5=3.5,
∴C(2,3.5)
设抛物线解析式为:y=a(x-2)2+3.5,
又∵抛物线过点B,
∴1.5=a(0-2)2+3.5
∴a=-
| 1 |
| 2 |
∴y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴所求抛物线解析式为:y=-
| 1 |
| 2 |
| 3 |
| 2 |
∵抛物线与x轴相交时,y=0,
∴0=-
| 1 |
| 2 |
| 3 |
| 2 |
∴x1=2+
| 7 |
| 7 |
∴D( 2+
| 7 |
∴水流落点D到A点的距离为:2+
| 7 |
故答案为:2+
| 7 |
点评:此题主要考查了二次函数的应用,根据所建坐标系的特点设合适的函数表达式形式进而求出二次函数解析式是解决问题的关键.

练习册系列答案
相关题目
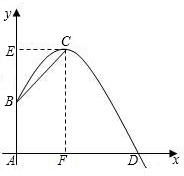 一自动喷灌设备的喷流情况如图所示,设水管AB在高出地面1.5米的B处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头B与水流最高点C连线成45°角,水流最高点C比喷头高2米,求水流落点D到A点的距离.
一自动喷灌设备的喷流情况如图所示,设水管AB在高出地面1.5米的B处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头B与水流最高点C连线成45°角,水流最高点C比喷头高2米,求水流落点D到A点的距离. 改革开放后,不少农村用上了自动喷灌设备.如图所示,AB表示水管,在B处有一个自动旋转的喷水头,一瞬间喷出的水是抛物线状,建立如图所示的直角坐标系后,抛物线的表达式为y=-
改革开放后,不少农村用上了自动喷灌设备.如图所示,AB表示水管,在B处有一个自动旋转的喷水头,一瞬间喷出的水是抛物线状,建立如图所示的直角坐标系后,抛物线的表达式为y=- 如图,AB是自动喷灌设备的水管,点A在地面,点B高出地面1.5米.在B处有一自动旋转的喷水头,在每一瞬间,喷出的水流呈抛物线状,喷头B与水流最高点C的连线与水平线成45°角,水流的最高点C与喷头B高出2米,在如图的坐标系中,水流的落地点D到点A的距离是________米.
如图,AB是自动喷灌设备的水管,点A在地面,点B高出地面1.5米.在B处有一自动旋转的喷水头,在每一瞬间,喷出的水流呈抛物线状,喷头B与水流最高点C的连线与水平线成45°角,水流的最高点C与喷头B高出2米,在如图的坐标系中,水流的落地点D到点A的距离是________米.