题目内容
【题目】(本题满分![]() 分)已知在平面直角坐标系
分)已知在平面直角坐标系![]() 中,点
中,点![]() 是抛物线
是抛物线![]() 上的一个动点,点
上的一个动点,点![]() 的坐标为
的坐标为![]() .
.
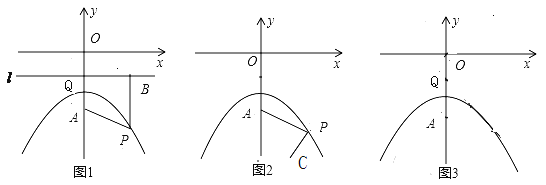
(1).如图1,直线![]() 过点
过点![]() 且平行于
且平行于![]() 轴,过
轴,过![]() 点作
点作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,猜想
,猜想![]() 与
与![]() 的大小关系:
的大小关系: ![]() ______
______ ![]() (填写“>”“<”或“=” ),并证明你的猜想.
(填写“>”“<”或“=” ),并证明你的猜想.
(2).请利用(1)的结论解决下列问题:
①.如图2,设点![]() 的坐标为
的坐标为![]() , 连接
, 连接![]() ,问
,问![]() 是否存在最小值?如果存在,请说明理由,并求出点
是否存在最小值?如果存在,请说明理由,并求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
②.若过动点![]() 和点
和点![]() 的直线交抛物线于另一点
的直线交抛物线于另一点![]() ,且
,且![]() ,求直线
,求直线![]() 的解析式(图3为备用图).
的解析式(图3为备用图).
【答案】(1)=;理由见解析;(2)①存在P点坐标为(2,﹣3);②y=![]() x﹣1或y=﹣
x﹣1或y=﹣![]() x﹣1.
x﹣1.
【解析】试题分析:(1)利用二次函数图象上点的坐标特征,设P(m,﹣![]() m2﹣2),则B(m,﹣1),然后根据两点间的距离公式计算出PA和PB,从而可判断它们相等;
m2﹣2),则B(m,﹣1),然后根据两点间的距离公式计算出PA和PB,从而可判断它们相等;
(2)①过点Q作QB∥x轴,过P点作PB⊥QB于B点,如图2,由(1)得PB=PA,根据两点之间线段最短,当点P、B、C共线时,此时P点的横坐标为2,然后计算对应的函数值即可得到P点坐标;
②过点Q(0,﹣1)作直线l平行于x轴,作PB⊥l于B,DE⊥l于E,如图3,由(1)得PB=PA,DE=DA,再证明△QDE∽△QPB,利用相似比得到![]() =
=![]() =
=![]() ,设P(m,﹣
,设P(m,﹣![]() m2﹣2),则B(m,﹣1),PB=
m2﹣2),则B(m,﹣1),PB=![]() m2+1,易得E点坐标为(
m2+1,易得E点坐标为(![]() m,﹣1),D点坐标为[
m,﹣1),D点坐标为[![]() m,﹣
m,﹣![]() (
(![]() m)2﹣2],则ED=
m)2﹣2],则ED=![]() m2+1,然后根据DE和PB的数量关系列方程
m2+1,然后根据DE和PB的数量关系列方程![]() m2+1=4(
m2+1=4(![]() m2+1),解方程求出m,从而得到P点坐标,最后利用待定系数法求直线PQ的解析式.
m2+1),解方程求出m,从而得到P点坐标,最后利用待定系数法求直线PQ的解析式.
解:(1)PA与PB相等.
理由如下:设P(m,﹣![]() m2﹣2),则B(m,﹣1),
m2﹣2),则B(m,﹣1),
∵PA=![]() =
=![]() =
=![]() m2+1,
m2+1,
PB=﹣1﹣(﹣![]() m2﹣2)=
m2﹣2)=![]() m2+1,
m2+1,
∴PA=PB.
故答案为=;
(2)①存在.
过点Q作QB∥x轴,过P点作PB⊥QB于B点,如图2,由(1)得PB=PA,则PA+PC=PB+PC,
当点P、B、C共线时,PB+PC最小,此时PC⊥QB,P点的横坐标为2,
当x=2时,y=﹣![]() x2﹣2=﹣
x2﹣2=﹣![]() ×4﹣2=﹣3,
×4﹣2=﹣3,
即此时P点坐标为(2,﹣3);
②过点Q(0,﹣1)作直线l平行于x轴,作PB⊥l于B,DE⊥l于E,如图3,由(1)得PB=PA,DE=DA,
∵PA=4AD,
∴PB=4DE,
∵DE∥PB,
∴△QDE∽△QPB,
∴![]() =
=![]() =
=![]() ,
,
设P(m,﹣![]() m2﹣2),则B(m,﹣1),PB=
m2﹣2),则B(m,﹣1),PB=![]() m2+1,
m2+1,
∴E点坐标为(![]() m,﹣1),D点坐标为[
m,﹣1),D点坐标为[![]() m,﹣
m,﹣![]() (
(![]() m)2﹣2],
m)2﹣2],
∴ED=﹣1+![]() (
(![]() m)2+2=
m)2+2=![]() m2+1,
m2+1,
∴![]() m2+1=4(
m2+1=4(![]() m2+1),解得m1=4,m2=﹣4,
m2+1),解得m1=4,m2=﹣4,
∴P点坐标为(4,﹣6)或(﹣4,﹣6),
当P点坐标为(4,﹣6)时,直线PQ的解析式为y=﹣![]() x﹣1,
x﹣1,
当P点坐标为(﹣4,﹣6)时,直线PQ的解析式为y=![]() x﹣1,
x﹣1,
即直线PQ的解析式为y=![]() x﹣1或y=﹣
x﹣1或y=﹣![]() x﹣1.
x﹣1.


 全优点练单元计划系列答案
全优点练单元计划系列答案