ƒøƒĞ»ı
°æƒø°øŒ ±≥æ∞
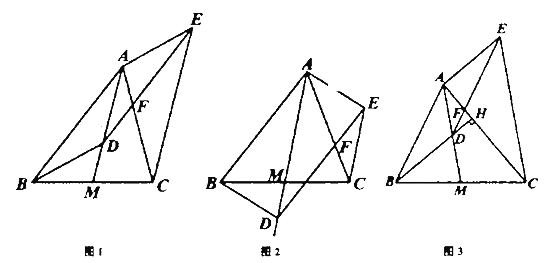
»ÁÕº£®1£©£¨‘ĞÀƒ±ş–ŒABCD÷–£¨°œB+°œD£Ω180°„£¨AB£ΩAD£¨°œBAD£Ω¶¡£¨“‘µ„AŒ™∂•µ„◊˜“ª∏ˆΩ«£¨Ω«µƒ¡Ω±ş∑÷±ΩªBC£¨CD”е„E£¨F£¨«“°œEAF![]() ¶¡£¨¡¨Ω”EF£¨ ‘ÃΩæø£∫œş∂ŒBE£¨DF£¨EF÷ƺ‰µƒ ˝¡øπÿœµ£Æ
¶¡£¨¡¨Ω”EF£¨ ‘ÃΩæø£∫œş∂ŒBE£¨DF£¨EF÷ƺ‰µƒ ˝¡øπÿœµ£Æ

£®1£©Ãÿ ‚«Èæ∞
‘Ğ…œ ˆÃº˛œ¬£¨–°√˜‘ˆº”ú˛°∞µ±°œBAD£Ω°œB£Ω°œD£Ω90°„ ±°±»ÁÕº£®2£©£¨–°√˜∫İøÏ–¥≥ˆ¡À£∫BE£¨DF£¨EF÷ƺ‰µƒ ˝¡øπÿœµŒ™______£Æ
£®2£©¿‡±»≤¬œÎ
¿‡±»Ãÿ ‚«Èæ∞£¨–°√˜≤¬œÎ£∫‘Ğ»ÁÕº£®1£©µƒÃº˛œ¬œş∂ŒBE£¨DF£¨EF÷ƺ‰µƒ ˝¡øπÿœµ «∑Ò»‘»ª≥…¡¢£ø»Ù≥…¡¢£¨«Îƒ„∞Ô÷˙–°√˜ÕÍ≥…÷§√˜£ª»Ù≤ª≥…¡¢£¨«ÎÀµ√˜¿Ì”…£Æ
£®3£©Ω‚戌 Â
»ÁÕº£®3£©£¨‘Ğ°˜ABC÷–£¨°œBAC£Ω90°„£¨AB£ΩAC£Ω4£¨µ„D£¨Eæ˘‘Ğ±şBC…œ£¨«“°œDAE£Ω45°„£¨»ÙBD![]() £¨«Î÷±Ω”–¥≥ˆDEµƒ≥§£Æ
£¨«Î÷±Ω”–¥≥ˆDEµƒ≥§£Æ
°æ¥∞∏°ø£®1£©BE+DF£ΩEF£ª£®2£©≥…¡¢£ª£®3£©DE![]()
°æΩ‚Œˆ°ø
£®1£©Ω´°˜ABE»∆µ„AƒÊ ±’Ζ˝◊™90°„£¨µ√µΩ°˜ADG£¨”…–˝◊™µƒ–‘÷ ø…µ√AE£ΩAG£¨BE£ΩDG£¨°œBAE£Ω°œDAG£¨∏˘æı°œEAF=![]() °œBADø…µ√°œBAE+°œDAF£Ω45°„£¨º¥ø…µ√≥ˆ°œ°œEAF£Ω°œFAG£¨¿˚”√SASø…÷§√˜°˜AFE°’°˜AFG£¨ø…µ√EF=FG£¨Ω¯∂¯ø…µ√EF=BE+FD£ª£®2£©Ω´°˜ABE»∆µ„AƒÊ ±’Ζ˝◊™¶¡µ√µΩ°˜ADH£¨”…–˝◊™µƒ–‘÷ ø…µ√°œABE£Ω°œADH£¨°œBAE£Ω°œDAH£¨AE£ΩAH£¨BE£ΩDH£¨∏˘æı°œBAD£Ω¶¡£¨°œEAF
°œBADø…µ√°œBAE+°œDAF£Ω45°„£¨º¥ø…µ√≥ˆ°œ°œEAF£Ω°œFAG£¨¿˚”√SASø…÷§√˜°˜AFE°’°˜AFG£¨ø…µ√EF=FG£¨Ω¯∂¯ø…µ√EF=BE+FD£ª£®2£©Ω´°˜ABE»∆µ„AƒÊ ±’Ζ˝◊™¶¡µ√µΩ°˜ADH£¨”…–˝◊™µƒ–‘÷ ø…µ√°œABE£Ω°œADH£¨°œBAE£Ω°œDAH£¨AE£ΩAH£¨BE£ΩDH£¨∏˘æı°œBAD£Ω¶¡£¨°œEAF![]() ¶¡ø…µ√°œBAE+°œFAD
¶¡ø…µ√°œBAE+°œFAD![]() ¶¡£¨Ω¯∂¯ø…÷§√˜°œFAH£Ω°œEAF£¨¿˚”√SASø…÷§√˜°˜AEF°’°˜AHF£¨ø…µ√EF=FH=BE+FD£ª£®3£©Ω´°˜AEC»∆µ„AÀ≥ ±’Ζ˝◊™90°„£¨µ√µΩ°˜AE°‰B£¨¡¨Ω”DE°‰£¨”…–˝◊™µƒ–‘÷ ø…µ√BE°‰£ΩEC£¨AE°‰£ΩAE£¨°œC£Ω°œABE°‰£¨°œEAC£Ω°œE°‰AB£¨∏˘æıµ»—¸÷±Ω«»˝Ω«–Œµƒ–‘÷ ø…µ√°œABC£Ω°œACB£Ω45°„£¨BC£Ω4
¶¡£¨Ω¯∂¯ø…÷§√˜°œFAH£Ω°œEAF£¨¿˚”√SASø…÷§√˜°˜AEF°’°˜AHF£¨ø…µ√EF=FH=BE+FD£ª£®3£©Ω´°˜AEC»∆µ„AÀ≥ ±’Ζ˝◊™90°„£¨µ√µΩ°˜AE°‰B£¨¡¨Ω”DE°‰£¨”…–˝◊™µƒ–‘÷ ø…µ√BE°‰£ΩEC£¨AE°‰£ΩAE£¨°œC£Ω°œABE°‰£¨°œEAC£Ω°œE°‰AB£¨∏˘æıµ»—¸÷±Ω«»˝Ω«–Œµƒ–‘÷ ø…µ√°œABC£Ω°œACB£Ω45°„£¨BC£Ω4![]() £¨º¥ø…«Û≥ˆ°œE°‰BD£Ω90°„£¨¿˚”√SASø…÷§√˜°˜AEF°’°˜AHF£¨ø…µ√DE£ΩDE°‰£¨¿˚”√π¥π…∂®¿Ì«Û≥ˆDEµƒ≥§º¥ø…µƒ¥∞∏.
£¨º¥ø…«Û≥ˆ°œE°‰BD£Ω90°„£¨¿˚”√SASø…÷§√˜°˜AEF°’°˜AHF£¨ø…µ√DE£ΩDE°‰£¨¿˚”√π¥π…∂®¿Ì«Û≥ˆDEµƒ≥§º¥ø…µƒ¥∞∏.
£®1£©BE+DF£ΩEF£¨
»ÁÕº1£¨Ω´°˜ABE»∆µ„AƒÊ ±’Ζ˝◊™90°„£¨µ√µΩ°˜ADG£¨
°ş°œADC£Ω°œB£Ω°œADG£Ω90°„£¨
°‡°œFDG£Ω180°„£¨º¥µ„F£¨D£¨Gπ≤œş£Æ
”…–˝◊™ø…µ√AE£ΩAG£¨BE£ΩDG£¨°œBAE£Ω°œDAG£Æ
°ş°œBAE+°œDAF£Ω°œBAD©Å°œEAF£Ω90°„©Å![]() °œBAD=90°„-45°„£Ω45°„£¨
°œBAD=90°„-45°„£Ω45°„£¨
°‡°œDAG+°œDAF£Ω45°„£¨º¥°œFAG=45°„£¨
°‡°œEAF£Ω°œFAG£¨
°‡°˜AFE°’°˜AFG£®SAS£©£¨
°‡EF£ΩFG£Æ
”÷°şFG£ΩDG+DF£ΩBE+DF£¨
°‡BE+DF£ΩEF£¨

π ¥∞∏Œ™£∫BE+DF£ΩEF£Æ
£®2£©≥…¡¢£Æ
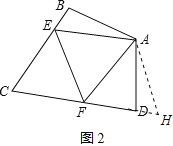
»ÁÕº2£¨Ω´°˜ABE»∆µ„AƒÊ ±’Ζ˝◊™¶¡µ√µΩ°˜ADH£¨
ø…µ√°œABE£Ω°œADH£¨°œBAE£Ω°œDAH£¨AE£ΩAH£¨BE£ΩDH£Æ
°ş°œB+°œADC£Ω180°„£¨
°‡°œADH+°œADC£Ω180°„£¨
°‡µ„C£¨D£¨H‘ĞÕ¨“ª÷±œş…œ£Æ
°ş°œBAD£Ω¶¡£¨°œEAF![]() ¶¡£¨
¶¡£¨
°‡°œBAE+°œFAD![]() ¶¡£¨
¶¡£¨
°‡°œDAH+°œFAD![]() ¶¡£¨
¶¡£¨
°‡°œFAH£Ω°œEAF£¨
”÷°şAF£ΩAF£¨
°‡°˜AEF°’°˜AHF£®SAS£©£¨
°‡EF£ΩFH£ΩDF+DH£ΩDF+BE£ª
£®3£©DE![]() £¨
£¨
»ÁÕº3£¨Ω´°˜AEC»∆µ„AÀ≥ ±’Ζ˝◊™90°„£¨µ√µΩ°˜AE°‰B£¨¡¨Ω”DE°‰£Æ
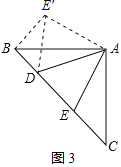
ø…µ√BE°‰£ΩEC£¨AE°‰£ΩAE£¨°œC£Ω°œABE°‰£¨°œEAC£Ω°œE°‰AB£¨
‘ĞRt°˜ABC÷–£¨°şAB£ΩAC£Ω4£¨°œBAC=90°„£¨
°‡°œABC£Ω°œACB£Ω45°„£¨BC£Ω4![]() £¨
£¨
°‡CD=BC=BD=3![]() £¨
£¨
°‡°œABC+°œABE°‰£Ω90°„£¨º¥°œE°‰BD£Ω90°„£¨
°‡E°‰B2+BD2£ΩE°‰D2£Æ
“◊÷§°˜AE°‰D°’°˜AED£¨
°‡DE£ΩDE°‰£¨
°‡DE2£ΩBD2+EC2£¨º¥DE2![]() £¨
£¨
Ω‚µ√![]() £Æ
£Æ

 ∫ƺŸÃϵÿ÷ÿ«Ï≥ˆ∞Ê…Áœµ¡–¥∞∏
∫ƺŸÃϵÿ÷ÿ«Ï≥ˆ∞Ê…Áœµ¡–¥∞∏