Question

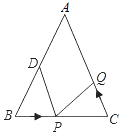
【题目】如图，DE是AB的垂直平分线．

（1）已知AC=5cm，△ADC的周长为17cm，则BC的长__________

（2）若AD平分∠BAC,AD=AC,则∠C= __________

Answer 1

【答案】12cm 72°

【解析】

（1）要求BC的大小，只要求出CD+BD，由线段的垂直平分线的性质知BD=AD，结合三角形的周长可得答案；

（2）设∠BAD=x．由垂直平分线的性质得到AD=BD，由等边对等角得到∠B=∠BAD=x，由三角形外角的性质得到∠ADC=∠B+∠BAD= 2x．由等腰三角形的性质得到∠C=∠ADC=2x．由角平分线的性质得到∠CAD=∠BAD=x．在△ADC中，由三角形内角和定理列方程得到x的值，即可得到结论．

（1）∵DE是边AB的垂直平分线，∴AD=BD，∴△ADC的周长=AD+DC+AC=BD+DC+AC=BC+AC=17cm．

又∵AC=5cm，∴BC=12cm．

（2）设∠BAD=x．

∵DE是边AB的垂直平分线，∴AD=BD，∴∠B=∠BAD=x，∴∠ADC=∠B+∠BAD=x+x=2x．

∵AD=AC，∴∠C=∠ADC=2x．

∵AD平分∠BAC，∴∠CAD=∠BAD=x．在△ADC中，x+2x+2x=180°，解得：x=36°，∴∠C=2x=72°．

故答案为：12cm，72°．