题目内容
如图,在直角坐标系xOy中,直线 与双曲线
与双曲线 相交于
相交于 、B
、B 两点,矩形
两点,矩形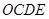 的边
的边 恰好被点
恰好被点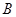 平分,边
平分,边 交双曲线于
交双曲线于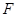 点,四边形
点,四边形 的面积为2.
的面积为2.
(1)求n的值;
(2)求不等式 的解集
的解集
(1)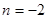 ;(2)
;(2) 的解集为
的解集为 .
.
解析试题分析:(1)先根据矩形性质和线段中点的坐标公式得到D(2b,﹣2),则矩形OCDE的面积=4b,再根据反比例函数的比例系数的几何意义得到S△OCB=S△OEF= |n|=﹣
|n|=﹣ n,然后利用四边形OBDF的面积=矩形OCDB﹣S△OCB﹣S△OEF,可求出n;
n,然后利用四边形OBDF的面积=矩形OCDB﹣S△OCB﹣S△OEF,可求出n;
(2)由于反比例解析式为y=﹣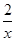 ,则B点坐标为(1,﹣2),再利用反比例函数的性质确定A点坐标为(﹣1,2),然后观察函数图象求解.
,则B点坐标为(1,﹣2),再利用反比例函数的性质确定A点坐标为(﹣1,2),然后观察函数图象求解.
试题解析:(1)连接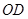 .
.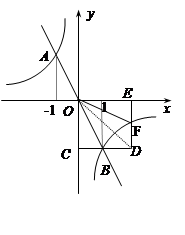
∵边 恰好被点
恰好被点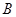 平分,
平分,
∴ ,
,
∵矩形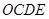 ,
,
∴
∵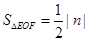 ,
,
∴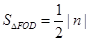
∴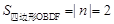 ,
,
∵双曲线分布在二、四象限,
∴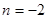 ;
;
(2)把 代入
代入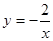 ,得
,得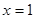 ,
,
∴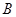 点的横坐标为1.
点的横坐标为1.
∵双曲线及过原点的直线均是关于原点成中心对称的图形
∴它们的交点也关于原点成中心对称,
∴ 点的横坐标为
点的横坐标为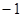 ,
,
由图像可知: 的解集为
的解集为 .
.
考点:反比例函数与一次函数的交点问题.

练习册系列答案
相关题目
某地区冬季干旱,康平社区每天需从外地调运饮用水60吨.有关部门紧急部署,从甲、乙两水厂调运饮用水到供水点,甲厂每天最多可调出40吨,乙厂每天最多可调出45吨.从两水厂运水到康平社区供水点的路程和运费如下表:
| | 到康平社区供水点的路程(千米) | 运费(元/吨·千米) |
| 甲厂 | 20 | 4 |
| 乙厂 | 14 | 5 |
(2)设从甲厂调运饮用水x吨,总运费为W元,试写出W关于x的函数关系式,并确定x的取值范围.怎样安排调运方案才能使每天的总运费最省?
 经过点(1,-1),求关于x的不等式2x-b≥0的解集.
经过点(1,-1),求关于x的不等式2x-b≥0的解集. 的图象在第四象限相交于点P,并且PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,-6)且S△DBP=27.
的图象在第四象限相交于点P,并且PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,-6)且S△DBP=27. 的图象与△ABP总有公共点,直接写出n的取值范围.
的图象与△ABP总有公共点,直接写出n的取值范围.
 x+6分别与x轴、y轴交于A、B两点;直线y=
x+6分别与x轴、y轴交于A、B两点;直线y= x与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿
x与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿 轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN,设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).
轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN,设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).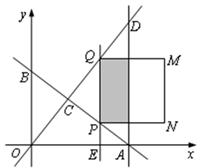
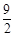 )在正方形PQMN内部时t的取值范围.
)在正方形PQMN内部时t的取值范围. 的图象经过点(
的图象经过点( ,
,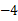 ),且与正比例函数
),且与正比例函数 的图象相交于点(4,
的图象相交于点(4, ),
), 、
、 的值;
的值; 轴相交得到的三角形的面积.
轴相交得到的三角形的面积. 的图象与y轴交于点A,一次函数
的图象与y轴交于点A,一次函数 的图象 经过点B(0,-1),并且与x轴以及
的图象 经过点B(0,-1),并且与x轴以及