题目内容
【题目】如图1,将一副直角三角板放在同一条直线AB上,其中![]() ,
,![]() .
.
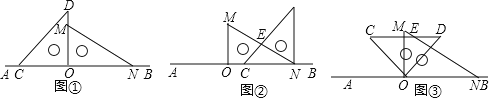
![]() 将图1中的三角尺OCD沿AB的方向平移至图
将图1中的三角尺OCD沿AB的方向平移至图![]() 的位置,使得点O与点N重合,CD与MN相交于点E,求
的位置,使得点O与点N重合,CD与MN相交于点E,求![]() 的度数;
的度数;
![]() 将图1中的三角尺OCD绕点O按顺时针方向旋转,使一边OD在
将图1中的三角尺OCD绕点O按顺时针方向旋转,使一边OD在![]() 的内部,如图3,且OD恰好平分
的内部,如图3,且OD恰好平分![]() ,CD与MN相交于点E,求
,CD与MN相交于点E,求![]() 的度数;
的度数;
![]() 将图1中的三角尺OCD绕点O按每秒
将图1中的三角尺OCD绕点O按每秒![]() 的速度沿顺时针方向旋转一周,在旋转的过程中,在第______ 秒时,边CD恰好与边MN平行;在第______ 秒时,直线CD恰好与直线MN垂直
的速度沿顺时针方向旋转一周,在旋转的过程中,在第______ 秒时,边CD恰好与边MN平行;在第______ 秒时,直线CD恰好与直线MN垂直![]() 直接写出结果
直接写出结果![]()
【答案】(1)105°;(2)见解析;(3) 5或17;11或23.
【解析】(1)根据三角形的内角和定理可得∠CEN=180°﹣∠DCN﹣∠MNO,代入数据计算即可得解;
(2)根据角平分线的定义求出∠DON=45°,利用内错角相等两直线平行求出CD∥AB,再根据两直线平行,同旁内角互补求解即可;
(3)①分CD在AB上方时,CD∥MN,设OM与CD相交于F,根据两直线平行,同位角相等可得∠OFD=∠M=60°,然后根据三角形的内角和定理列式求出∠MOD,即可得解;CD在AB的下方时,CD∥MN,设直线OM与CD相交于F,根据两直线平行,内错角相等可得∠DFO=∠M=60°,然后利用三角形的内角和定理求出∠DOF,再求出旋转角即可;②分CD在OM的右边时,设CD与AB相交于G,根据直角三角形两锐角互余求出∠CGN,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CON,再求出旋转角即可,CD在OM的左边时,设CD与AB相交于G,根据直角三角形两锐角互余求出∠NGD,再根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠AOC,然后求出旋转角,计算即可得解.
(1)在△CEN中,∠CEN=180°﹣∠DCN﹣∠MNO
=180°﹣45°﹣30°
=105°;
(2)∵OD平分∠MON,∴∠DON=![]() ∠MPN=
∠MPN=![]() ×90°=45°,∴∠DON=∠D=45°,∴CD∥AB,∴∠CEN=180°﹣∠MNO=180°﹣30°=150°;
×90°=45°,∴∠DON=∠D=45°,∴CD∥AB,∴∠CEN=180°﹣∠MNO=180°﹣30°=150°;
(3)如图1,CD在AB上方时,设OM与CD相交于F.
∵CD∥MN,∴∠OFD=∠M=60°.在△ODF中,∠MOD=180°﹣∠D﹣∠OFD=180°﹣45°﹣60°=75°,∴旋转角为75°,t=75°÷15°=5秒;
CD在AB的下方时,设直线OM与CD相交于F.
∵CD∥MN,∴∠DFO=∠M=60°.在△DOF中,∠DOF=180°﹣∠D﹣∠DFO=180°﹣45°﹣60°=75°,∴旋转角为75°+180°=255°,t=255°÷15°=17秒;
综上所述:第5或17秒时,边CD恰好与边MN平行;
如图2,CD在OM的右边时,设CD与AB相交于G.
∵CD⊥MN,∴∠NGC=90°﹣∠MNO=90°﹣30°=60°,∴∠CON=∠NGC﹣∠OCD=60°﹣45°=15°,∴旋转角为180°﹣∠CON=180°﹣15°=165°,t=165°÷15°=11秒,CD在OM的左边时,设CD与AB相交于G.
∵CD⊥MN,∴∠NGD=90°﹣∠MNO=90°﹣30°=60°,∴∠AOC=∠NGD﹣∠C
综上所述:第11或23秒时,直线CD恰好与直线MN垂直.
故答案为:5或17;11或23.


【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
学生最喜欢的活动项目的人数统计表
项目 | 学生数(名) | 百分比 |
丢沙包 | 20 | 10% |
打篮球 | 60 | p% |
跳大绳 | n | 40% |
踢毽球 | 40 | 20% |
根据图表中提供的信息,解答下列问题:
(1)m= ,n= ,p= ;
(2)请根据以上信息直接补全条形统计图;

(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳.