题目内容
【题目】在所给图形中:
⑴求证:∠BDC=∠A+∠B+∠C;
⑵如果点D与点A分别在线段BC的两侧,猜想∠BDC、∠A、∠B、∠C这4个角之间有怎样的关系,并证明你的结论.

【答案】(1)证明见解析;
(2)![]() ,证明见解析
,证明见解析
【解析】试题分析:(1)根据三角形外角性质得出∠BDE=∠BAD+∠B,∠CDE=∠CAD+∠C,相加即可得出答案;(2)根据三角形内角和定理求出即可.
试题解析:1)证明:
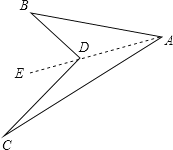
过D作射线AE,
∵∠BDE=∠BAD+∠B,∠CDE=∠CAD+∠C,
∴∠BDC=∠BDE+∠CDE=∠BAD+∠B+∠CAD+∠C,
即∠BDC=∠BAC+∠B+∠C;
(2)猜想:∠B+∠BCD+∠BAD+∠D=360.
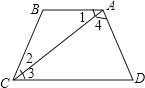
证明:∠B+∠BCC+∠D+∠BAD
=∠3+∠2+∠B+∠D+∠4+∠1
=(∠B+∠2+∠1)+(∠D+∠3+∠4)
=180°+180°=360°

练习册系列答案
相关题目





