题目内容
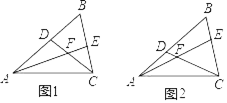
【题目】如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.

(1)求证:AE=EF.
(2)(探究1)变特殊为一般:若题中“点E是边BC的中点”变为“点E是BC边上任意一点”,则上述结论是否仍然成立?(填“是”或“否”).
(3)(探究2)在探究1的前提下,若题中结论“AE=EF”与条件“CF是正方形外角的平分线”互换,则命题是否还成立?请给出证明.
【答案】(1)见解析;(2)是;(3)仍然成立,见解析
【解析】
(1)取AB中点M,连接EM,求出BM=BE,得出∠BME=45°,求出∠AME=∠ECF=135°,求出∠MAE=∠FEC,根据ASA推出△AME和△ECF全等即可;
(2)截取BE=BM,连接EM,求出AM=EC,得出∠BME=45°,求出∠AME=∠ECF=135°,求出∠MAE=∠FEC,根据ASA推出△AME和△ECF全等即可;
(3)过点F作FH⊥BC,交BC的延长线于点H,得到∠BAE=∠HEF,再证明△ABE≌△EHF可得出BE=CH,FH=CH,从而得到∠HFC=∠DCF=45°,即可得出结论.
解:(1)证明:取AB的中点M,连接ME,如图1,
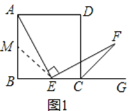
∴AM=BM=![]() AB.
AB.
∵E是BC的中点,
∴BE=EC=![]() BC.
BC.
∵四边形ABCD是正方形,
∴∠B=∠BCD=90°,AB=BC.
∴AM=EC,BM=BE.
∴∠BME=45°.
∴∠AME=135°.
又∵CF是正方形外角的平分线,
∴∠ECF=135°.
∵∠AEF=90°,
∴∠AEB+∠FEC=90°.
又∵∠AEB+∠BAE=90°,
∴∠BAE=∠FEC.
∴△AME≌△ECF(ASA).
∴AE=EF.
(2)【探究1】变特殊为一般:若题中“点E是边BC的中点”变为“点E是BC边上任意一点”,则上述结论仍然成立.
理由是:如图2,在AB上截取BM=BE,连接ME,
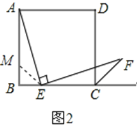
∵∠B=90°,
∴∠BME=∠BEM=45°,
∴∠AME=135°=∠ECF,
∵AB=BC,BM=BE,
∴AM=EC,
在△AME和△ECF中
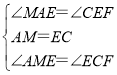 ,
,
∴△AME≌△ECF(ASA),
∴AE=EF;
(3)【探究2】在探究1的前提下,若题中结论“AE=EF”与条件“CF是正方形外角的平分线”互换,则命题仍然成立.
证明:过点F作FH⊥BC,交BC的延长线于点H,如图3,

∵∠AEF=90°,
∴∠AEB+∠FEH=90°.
∵∠ABE=90°,
∴∠AEB+∠BAE=90°.
∴∠BAE=∠HEF.
在△ABE和△EHF中,
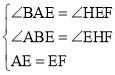
∴△ABE≌△EHF(AAS).
∴BE=HF,AB=EH=BC.
∴BC-EC=EH-EC,即BE=CH.
∴HF=CH.
∴∠HCF=∠HFC=45°,∠DCF=45°.
∴CF是正方形外角的平分线.

【题目】校学生会对七年级部分学生的课外阅读量进行了随机调查,整理调查结果,并根据调查结果绘制了不完整的图表,如图所示:
本数(本) | 频数(人数) | 频率 |
5 | a | 0.3 |
6 | 10 | 0.2 |
7 | 20 | b |
8 | 5 | 0.1 |
合计 | c | 1 |
(1)统计表中的b= ,c= ;请将频数分布直方图补充完整.
(2)所有被调查学生课外阅读的平均本数为 本,课外阅读书本数的中位数为 本.
(3)若该校七年级共有1200名学生,估计该校七年级学生课外阅读6本及以下的人数为 人.