题目内容
阅读下面的材料:小明在研究中心对称问题时发现:
如图1,当点A1为旋转中心时,点P绕着点A1旋转180°得到P1点,点P1再绕着点A1旋转180°得到P2点,这时点P与点P2重合.
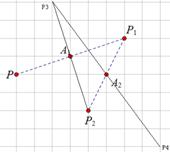
如图2,当点A1、A2为旋转中心时,点P绕着点A1旋转180°得到P1点,点P1绕着点A2旋转180°得到P2点,点P2绕着点A1旋转180°得到P3点,点P3绕着点A2旋转180°得到P4点,小明发现P、P4两点关于点P2中心对称.
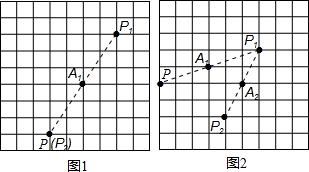
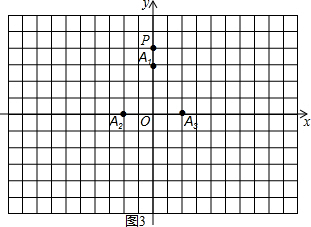
(1)请在图2中画出点P3、P4,小明在证明P、P4两点关于点P2中心对称时,除了说明P、P2、P4三点共线之外,还需证明
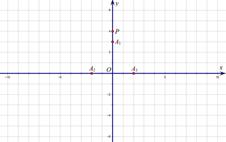
(2)如图3,在平面直角坐标系xOy中,当A1(0,3)、A2(-2,0)、A2(2,0)为旋转中心时,点P(0,4)绕着点A1旋转180°得到P1点;点P1绕着点A2旋转180°得到P2点;点P2绕着点A3旋转180°得到P3点;点P3绕着点A1旋转180°得到点p4点….继续如此操作若干次得到点P5、P6、…,则点P2的坐标为
分析:(1)根据图形结合对称的定义得出答案;
(2)利用已知得出对应点坐标,进而得出P点坐标变换规律进而得出答案.
(2)利用已知得出对应点坐标,进而得出P点坐标变换规律进而得出答案.
解答: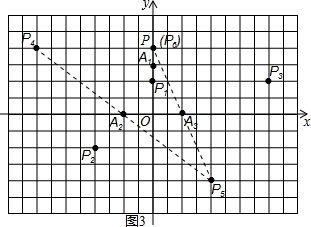
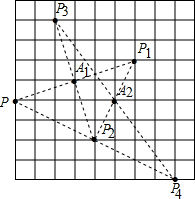 解:(1)如图,除了证P、P2、P4三点共线外,还要证PP2=P2P4,
解:(1)如图,除了证P、P2、P4三点共线外,还要证PP2=P2P4,
故答案为:PP2=P2P4;
(2)如图所示:
点P2的坐标为:(-4,-2),
∵由图形可得出:P点与P6重合,
∴P点每6次循环一周,
∵2017÷6=336…1,
∴点P2017的坐标与P1坐标相同为:(0,2),
故答案为:(-4,-2),(0,2).

 解:(1)如图,除了证P、P2、P4三点共线外,还要证PP2=P2P4,
解:(1)如图,除了证P、P2、P4三点共线外,还要证PP2=P2P4,故答案为:PP2=P2P4;
(2)如图所示:
点P2的坐标为:(-4,-2),
∵由图形可得出:P点与P6重合,
∴P点每6次循环一周,
∵2017÷6=336…1,
∴点P2017的坐标与P1坐标相同为:(0,2),
故答案为:(-4,-2),(0,2).
点评:此题主要考查了几何变换以及点的坐标确定位置,得出P点坐标变化规律是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
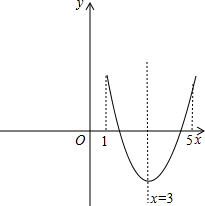 阅读下面的材料:
阅读下面的材料: 的最大值.他画图研究后发现,
的最大值.他画图研究后发现, 和
和 时的函数值相等,于是他认为需要对
时的函数值相等,于是他认为需要对 进行分类讨论.
进行分类讨论.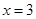 ,
,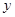 的最大值为2;
的最大值为2;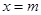 时,
时,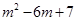 .
.
 ≤x≤4时,二次函数
≤x≤4时,二次函数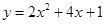 的最大值为_______;
的最大值为_______;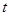 的值为_______.
的值为_______.







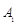 为旋转中心时,点
为旋转中心时,点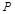 绕着点
绕着点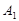 旋转180°得到
旋转180°得到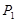 点,点
点,点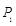 再绕着点
再绕着点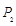 点,这时点
点,这时点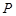 与点
与点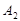 为旋转中心时,点
为旋转中心时,点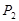 点,点
点,点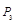 点,点
点,点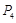 点,小明发现P、
点,小明发现P、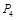 两点关于点
两点关于点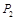 中心对称.
中心对称.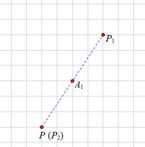
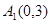 、
、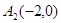 、
、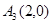 为旋转中心时,点
为旋转中心时,点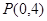 绕着点
绕着点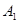 旋转180°得到
旋转180°得到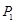 点;点
点;点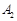 旋转180°得到
旋转180°得到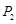 点;点
点;点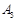 旋转180°得到
旋转180°得到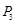 点;点
点;点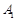 旋转180°得到点
旋转180°得到点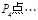 . 继续如此操作若干次得到点
. 继续如此操作若干次得到点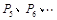 ,则点
,则点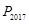 的坐为.
的坐为.