题目内容
【题目】求证:等腰三角形底边上任一点到两腰的距离之和等于腰上的高.
【答案】(1)证明见解析.
【解析】试题分析:根据三角形的面积公式S△=![]() 底×高求得S△ABD、S△ACD、S△ABC;又由图易知,S△ABC=S△ABD+S△ACD,分析到这里,问题就迎刃而解了.
底×高求得S△ABD、S△ACD、S△ABC;又由图易知,S△ABC=S△ABD+S△ACD,分析到这里,问题就迎刃而解了.
试题解析:已知:△ABC中,AB=AC,D为BC上任意一点,DE⊥AB,DF⊥AC,垂足为E.F,CG⊥AB于G,
求证:CG=DE+DF.
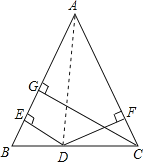
证明:已知如图所示。
∵ED⊥AB,
∴S△ABD=![]() ABED;
ABED;
∵DF⊥AC,
∴S△ACD=![]() ACDF;
ACDF;
∵CG⊥AB,
∴S△ABC=![]() ABCG;
ABCG;
又∵AB=AC,S△ABC=S△ABD+S△ACD,
∴![]() ABCG=
ABCG=![]() ABED+
ABED+![]() ACDF,
ACDF,
∴CG=DE+DF.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目