题目内容
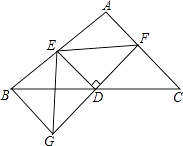
【题目】如图所示,四边形EFGH是由矩形ABCD的外角平分线围成的. 求证:四边形EFGH是正方形.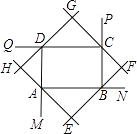
【答案】证明:∵矩形的ABCD的外角都是直角,HE,EF都是外角平分线, ∴∠BAE=∠ABE=45°.
∴∠E=90°.
同理,∠F=∠G=90°.
∴四边形EFGH为矩形.
∵AD=BC,∠HAD=∠HDA=∠FBC=∠FCB=45°,
∴△ADH≌△BCF(AAS).
∴AH=BF.
又∵∠EAB=∠EBA,
∴AE=BE.
∴AE+AH=EB+BF,即EH=EF.
∴矩形EFGH是正方形
【解析】由于四边形EFGH是由矩形ABCD的外角平分线围成,故先求出相关角的度数,再根据正方形的判定定理即可证得.
【考点精析】本题主要考查了矩形的性质和正方形的判定方法的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角才能正确解答此题.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目