题目内容
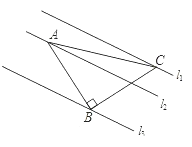
【题目】如图,正方形ABCD的边长为6,点E,F分别在边AB,BC上,若F是BC的中点,且∠EDF=45°,则DE的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
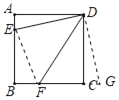
延长F至G,使CG=AE,连接DG,由SAS证明△ADE≌△CDG,得出DE=DG,∠ADE=∠CDG,再证明△EDF≌△GDF,得出EF=GF,设AE=CG=x,则EF=GF=3+x,在Rt△BEF中,由勾股定理得出方程,解方程得出AE=2,在Rt△ADE中,由勾股定理求出DE即可.
解:延长F至G,使CG=AE,连接DG、EF,如图所示:
∵四边形ABCD是正方形,
∴AD=AB=BC=CD=6,∠A=∠B=∠DCF=∠ADC=90°,
∴∠DCG=90°,
在△ADE和△CDG中,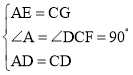 ,
,
∴△ADE≌△CDG(SAS),
∴DE=DG,∠ADE=∠CDG,
∴∠EDG=∠CDE+∠CDG=∠CDE+∠ADE=90°,
∵∠EDF=45°,
∴∠GDF=45°,
在△EDF和△GDF中,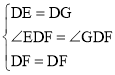 ,
,
∴△EDF≌△GDF(SAS),
∴EF=GF,
∵F是BC的中点,
∴BF=CF=3,
设AE=CG=x,则EF=GF=3+x,
在Rt△BEF中,由勾股定理得:32+(6﹣x)2=(3+x)2,
解得:x=2,即AE=2,
在Rt△ADE中,由勾股定理得:DE=![]() ;
;
故选:B.

 名校课堂系列答案
名校课堂系列答案【题目】某单位需以“挂号信”或“特快专递”方式向五所学校各寄一封信,这五封信的重量分别是![]() .根据这五所学校的地址及信件的重量范围,在邮局查得相关邮费标准如下:
.根据这五所学校的地址及信件的重量范围,在邮局查得相关邮费标准如下:
业务种类 | 计费单位 | 资费标准/元 | 挂号费/(元/封) | 特制信封(元/个) |
挂号信 | 首重100g,每重20g | 0.8 | 3 | 0.5 |
续重101~2000g,每重100g | 2.00 | |||
特制信封 | 首重1000g内 | 5.00 | 3 | 1.0 |
(1)重量为90g的信若以“挂号信”方式寄出,邮寄费为多少元?若以“特快专递”方式寄出呢?
(2)这五封信分别以怎样的方式寄出最合算?请说明理由.
(3)通过解答上述问题,你有何启示?(请你用一两句话说明)

【题目】问题背景:
小红同学在学习过程中遇到这样一道计算题“计算4×2.112-4×2.11×2.22+2.222”,她觉得太麻烦,估计应该有可以简化计算的方法,就去请教崔老师.崔老师说:你完成下面的问题后就可能知道该如何简化计算啦!
获取新知:
请你和小红一起完成崔老师提供的问题:
(1)填写下表:
x=-1,y=1 | x=1,y=0 | x=3,y=2 | x=2,y=-1 | x=2,y=3 | |
A=2x-y | -3 | 2 | 4 | 5 | 1 |
B=4x2-4xy+y2 | 9 | 4 | 16 |
(2)观察表格,你发现A与B有什么关系?
解决问题:
(3)请利用A与B之间的关系计算:4×2.112-4×2.11×2.22+2.222.