题目内容
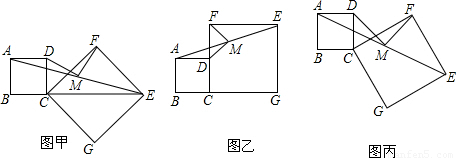
(2010•博野县三模)如图甲,操作:把正方形CGEF的对角线,CE放在正方形ABCD的边BC的延长线上(CG>BC),取线段AE的中点M.(1)探究线段MD、MF的位置及数量关系,直接写出答案即可;
(2)将正方形CGEF绕点C逆时针旋转45°(如图乙),令CG=2BC其他条件不变,结论是否发生变化,并加以证明;
(2)将正方形CGEF绕点C旋转任意角度后(如图丙),其他条件不变.探究:线段MD,MF的位置及数量关系,并加以证明.
【答案】分析:(1)利用测量或观察的方法即可作出判断;
(2)易证明△AMD≌△EMN,得到AD=EN,MD=MN,再根据CF=2AD,EF=2EN,得到:FD=FN.从而证得FM⊥MD,MF=MD;
(3)延长DM到N,使MN=MD,连接FD、FN、EN,延长EN与DC延长线交于点H.证明△DCF≌△NEF,即可得到线段MD,MF的位置及数量关系.
解答: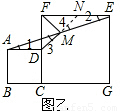 解:(1)MD=MF,MD⊥MF;(2分)
解:(1)MD=MF,MD⊥MF;(2分)
(2)结论不变MD=MF,MD⊥MF,
证明:如图乙,延长DM交FE于N.
∵正方形ABCD、CGEF,
∴CF=EF,AD=DC,∠CFE=90°,AD∥FE,
∴∠1=∠2.
在△AMD与△EMN中,
∵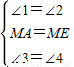 ,
,
∴△AMD≌△EMN,
∴AD=EN,MD=MN,
∵CF=2AD,EF=2EN,
∴FD=FN.
又∵∠DFN=90°,
∴FM⊥MD,MF=MD;(6分)
(3)MD=MF,MD⊥MF,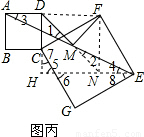
证法一:如图丙,延长DM到N,
使MN=MD,连接FD、FN、EN,
延长EN与DC延长线交于点H.
在△AMD与△EMN中,
∵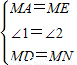 ,
,
∴△AMD≌△EMN,
∴∠3=∠4,AD=NE.
又∵正方形ABCD、CGEF,
∴CF=EF,AD=DC,∠ADC=90°,
∠CFE=∠ADC=∠FEG=∠FCG=90°.
∴DC=NE.
∵∠3=∠4,
∴AD∥EH.
∴∠H=∠ADC=90°.
∵∠G=90°,∠5=∠6,
∴∠7=∠8.
∵∠7+∠DCF=∠8+∠FEN=90°,
∴∠DCF=∠FEN.
在△DCF与△NEF中,
∵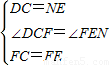 ,
,
∴△DCF≌△NEF,
∴FD=FN,∠DFC=∠NFE.
∵∠CFE=90°,
∴∠DFN=90°,
∴FM⊥MD,MF=MD.(10分)
证法二:如图丙,过点E作AD的平行线分别交DM、DC的延长线于N、H,连接DF、FN.
∴∠ADC=∠H,∠3=∠4.
∵AM=ME,∠1=∠2,
∴△AMD≌△EMN,
∴DM=NM,AD=EN.
∵四边形ABCD、四边形CGEF是正方形,
∴AD=DC,FC=FE,∠ADC=∠FCG=∠CFE=90°,
∴∠H=90°,∠5=∠NEF,DC=NE.
∴∠DCF+∠7=∠5+∠7=90°,
∴∠DCF=∠5=∠NEF.
在△DCF与△NEF中,
∵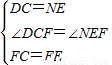 ,
,
∴△DCF≌△NEF.
∴FD=FN,∠DFC=∠NFE,
∵∠CFE=90°,
∴∠DFN=90°,
∴FM⊥MD,MF=MD.(10分)
点评:本题考查旋转的性质--旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.
(2)易证明△AMD≌△EMN,得到AD=EN,MD=MN,再根据CF=2AD,EF=2EN,得到:FD=FN.从而证得FM⊥MD,MF=MD;
(3)延长DM到N,使MN=MD,连接FD、FN、EN,延长EN与DC延长线交于点H.证明△DCF≌△NEF,即可得到线段MD,MF的位置及数量关系.
解答:
 解:(1)MD=MF,MD⊥MF;(2分)
解:(1)MD=MF,MD⊥MF;(2分)(2)结论不变MD=MF,MD⊥MF,
证明:如图乙,延长DM交FE于N.
∵正方形ABCD、CGEF,
∴CF=EF,AD=DC,∠CFE=90°,AD∥FE,
∴∠1=∠2.
在△AMD与△EMN中,
∵
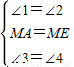 ,
,∴△AMD≌△EMN,
∴AD=EN,MD=MN,
∵CF=2AD,EF=2EN,
∴FD=FN.
又∵∠DFN=90°,
∴FM⊥MD,MF=MD;(6分)
(3)MD=MF,MD⊥MF,

证法一:如图丙,延长DM到N,
使MN=MD,连接FD、FN、EN,
延长EN与DC延长线交于点H.
在△AMD与△EMN中,
∵
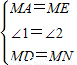 ,
,∴△AMD≌△EMN,
∴∠3=∠4,AD=NE.
又∵正方形ABCD、CGEF,
∴CF=EF,AD=DC,∠ADC=90°,
∠CFE=∠ADC=∠FEG=∠FCG=90°.
∴DC=NE.
∵∠3=∠4,
∴AD∥EH.
∴∠H=∠ADC=90°.
∵∠G=90°,∠5=∠6,
∴∠7=∠8.
∵∠7+∠DCF=∠8+∠FEN=90°,
∴∠DCF=∠FEN.
在△DCF与△NEF中,
∵
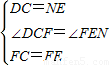 ,
,∴△DCF≌△NEF,
∴FD=FN,∠DFC=∠NFE.
∵∠CFE=90°,
∴∠DFN=90°,
∴FM⊥MD,MF=MD.(10分)
证法二:如图丙,过点E作AD的平行线分别交DM、DC的延长线于N、H,连接DF、FN.
∴∠ADC=∠H,∠3=∠4.
∵AM=ME,∠1=∠2,
∴△AMD≌△EMN,
∴DM=NM,AD=EN.
∵四边形ABCD、四边形CGEF是正方形,
∴AD=DC,FC=FE,∠ADC=∠FCG=∠CFE=90°,
∴∠H=90°,∠5=∠NEF,DC=NE.
∴∠DCF+∠7=∠5+∠7=90°,
∴∠DCF=∠5=∠NEF.
在△DCF与△NEF中,
∵
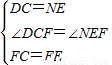 ,
,∴△DCF≌△NEF.
∴FD=FN,∠DFC=∠NFE,
∵∠CFE=90°,
∴∠DFN=90°,
∴FM⊥MD,MF=MD.(10分)
点评:本题考查旋转的性质--旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目

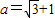 ,求
,求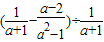 的值.
的值.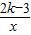 的图象在每个象限内,y随x的增大而增大,则k .
的图象在每个象限内,y随x的增大而增大,则k .