��Ŀ����
����Ŀ����������ABCD�ı�AB����ȡһ��E����EF��AB��BD�ڵ�F��ȡFD���е�G������EG��CG����ͼ��1������֤ EG=CG��EG��CG��
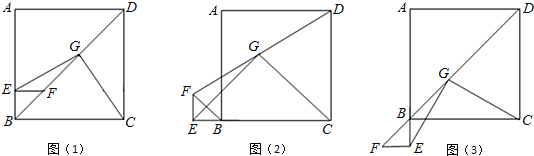
��1������BEF�Ƶ�B��ʱ����ת90�㣬��ͼ��2�������߶�EG��CG��������������ϵ��λ�ù�ϵ����ֱ��д����IJ��룮
��2������BEF�Ƶ�B��ʱ����ת180�㣬��ͼ��3�������߶�EG��CG����������������ϵ��λ�ù�ϵ����д����IJ��룬������֤����
���𰸡���1��EG=CG��EG��CG����2��EG��CG��������
��������
�����������ͼ��1����Ѱ��֤�����۵�˼·���ӳ�FE��DC����M����MG���������GFE�ա�GMC���ý��ۣ���ͼ��2������3���н���˽֤ⷨ����
�⣺��1��EG=CG��EG��CG��
��2��EG=CG��EG��CG��
֤�����ӳ�FE��DC�ӳ�����M����MG��
�ߡ�AEM=90������EBC=90�㣬��BCM=90����
���ı���BEMC�Ǿ��Σ�
��BE=CM����EMC=90����
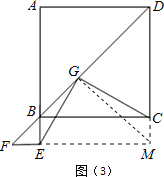
��ͼ��3����֪��
��BDƽ����ABC����ABC=90����
���EBF=45����
����EF��AB��
���BEFΪ����ֱ��������
��BE=EF����F=45����
��EF=CM��
�ߡ�EMC=90����FG=DG��
��MG=![]() FD=FG��
FD=FG��
��BC=EM��BC=CD��
��EM=CD��
��EF=CM��
��FM=DM��
����FG=DG��
��CMG=![]() ��EMC=45����
��EMC=45����
���F=��GMC��
������GFE����GMC�� ��
��
���GFE�ա�GMC��SAS����
��EG=CG����FGE=��MGC.
�ߡ�FMC=90����MF=MD��FG=DG��
��MG��FD��
���FGE+��EGM=90����
���MGC+��EGM=90����
����EGC=90����
��EG��CG��

 ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д� �����ܾ�ϵ�д�
�����ܾ�ϵ�д� ���ƿ�����ϵ�д�
���ƿ�����ϵ�д� ���¿쳵����������ϵ�д�
���¿쳵����������ϵ�д�