Question

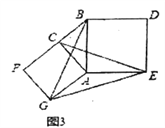
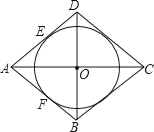
【题目】如图，已知⊙O与等腰△ABD的两腰AB、AD分别相切于点E、F，连接AO并延长到点C，使OC=AO，连接CD、CB．

（1）试判断四边形ABCD的形状，并说明理由；

（2）若AB=4cm，填空：

①当⊙O的半径为 　cm时，△ABD为等边三角形；

②当⊙O的半径为　 　cm时，四边形ABCD为正方形．

Answer 1

【答案】（1）菱形，理由见解析；（2）①；②2.

【解析】分析：（1）由AB、AD分别相切于点E、F，得到∠EAO=∠FAO，于是得到OD=OB，根据AO=OC，推出四边形ABCD是平行四边形，于是得到结论；

（2）①连接OE由切线的性质得到OE⊥AD，由△ABD为等边三角形，得到BD=AB=AD=4，根据直角三角形的性质得到结论由正方形的性质得到∠DAO=∠ADO=45°，由AD=AB=4，得到OA=OD=2，根据等腰直角三角形的性质即可得到结论．

详解：（1）四边形ABCD是菱形，

理由如下：∵AB、AD分别相切于点E、F，

∴∠EAO=∠FAO，

∴OD=OB，

∵AO=OC，

∴四边形ABCD是平行四边形，

∵AB=AD，

∴ABCD是菱形；

（2）①当⊙O的半径为时，△ABD为等边三角形；

连接OE，∵AD切⊙O于点E，

∴OE⊥AD，

∵△ABD为等边三角形，

∴BD=AB=AD=4，

∴∠DAO=30°，

∴OD=BD=2，AO=2，

∴OE=AO=，

∴当⊙O的半径为时，△ABD为等边三角形；

故答案为：；

②当⊙O的半径为2cm时，四边形ABCD为正方形；

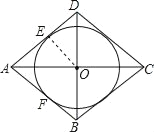
如图，∴∠DAO=∠ADO=45°，

∵AD=AB=4，

∴OA=OD=2，

由（2）知，OE⊥AD，

∴OE=AE=2，

∴当⊙O的半径为2cm时，四边形ABCD为正方形；

故答案为：2．