题目内容
24、附加题：已知直线y=b（b为实数）与函数y=|x|2-4|x|+3的图象至少有三个公共点，则实数b的取值范围
-1＜b≤3
．分析：用描点法，画出函数y=|x|2-4|x|+3的图象，①x≥0时，y=x2-4x+3=（x-2）2-1；②x＜0时，y=x2+4x+3=（x+2）2-1．①和②的图象关于x=0的直线成轴对称图形．又至少有三个公共点，从而可确定实数b的取值范围-1＜b≤3．
解答：解：由函数y=|x|2-4|x|+3，得：①x≥0时，y=x2-4x+3=（x-2）2-1；
②x＜0时，y=x2+4x+3=（x+2）2-1．x=0时y=3；x=±2时，顶点y=-1．①和②的图象关于x=0的直线成轴对称图形．
∵直线y=b（b为实数）与函数y=|x|2-4|x|+3的图象至少有三个公共点，
∴实数b的取值范围-1＜b≤3．
②x＜0时，y=x2+4x+3=（x+2）2-1．x=0时y=3；x=±2时，顶点y=-1．①和②的图象关于x=0的直线成轴对称图形．
∵直线y=b（b为实数）与函数y=|x|2-4|x|+3的图象至少有三个公共点，
∴实数b的取值范围-1＜b≤3．
点评：本题解答的关键是对直线和二次函数图象的掌握．
练习册系列答案
相关题目
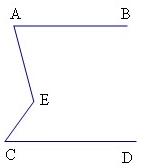24、附加题：已知，直线AB∥CD．
（附加题）已知：抛物线y=ax2+bx+c与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，点C在y轴的正半轴上，线段OB、OC的长（OB＜OC）是方程x2-10x+16=0的两个根，且抛物线的对称轴是直线x=-2．