Question

如图所示，O是直线AB上一点，∠COB=46°，OD平分∠AOC，OE平分∠COB，则∠DOE=______，如果将上题中∠COB=46°这个条件去掉，是否还能求出∠DOE的度数呢？如果可以求出，请写出求解过程．

Answer 1

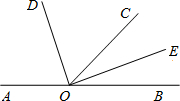
∵∠COB=46°，
∴∠AOC=180°-∠COB=180°-46°=134°，
∵OD平分∠AOC，OE平分∠COB，
∴∠COD=

1

2

∠AOC=

1

2

×134°=67°，
∠COE=

1

2

∠BOC=

1

2

×46°=23°，
∴∠DOE=∠COD+∠COE=67°+23°=90°；

能求出∠DOE=90°．
∵OD平分∠AOC，OE平分∠COB，
∴∠COD=

1

2

∠AOC，
∠COE=

1

2

∠BOC，
∴∠DOE=∠COD+∠COE=

1

2

（∠AOC+∠BOC）=

1

2

×180°=90°．