Question

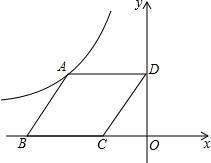已知，如图，菱形ABCD的一边BC在x轴上，且C点坐标为（-1，0），D点坐标（0，

3

）．反比例函数y=

k

x

过菱形的顶点A．
（1）求反比例函数的解析式；
（2）若P为反比例函数在第四象限的图象上一点，点Q在x轴上，问是否存在点P、Q，使得四边形CDQP为矩形？若存在，求出P和Q的坐标；若不存在，说明理由．

Answer 1

分析：（1）先根据C（-1，0），D（0，

3

）求出CD的长，进而得出A点坐标，再把A点坐标代入反比例函数y=

k

x

即可求出k的值，进而得出反比例函数的解析式；
（2）设Q（x，0），P（a，b），在Rt△CDQ中根据勾股定理可求出x的值，进而得出Q点的坐标，设矩形CDQP的中点为O，求出O点坐标，再根据线段DP的中点也是O点即可得出点P的坐标．

解答：解：（1）∵C（-1，0），D（0，

3

），
∴CD=

(-1)2+( 3 )

2=2，
∴A（-2，

3

），
∵点A在反比例函数y=

k

x

上，
∴k=（-2）×

3

=-2

3

，
∴反比例函数的解析式为：y=-

2 3

x

；

（2）存在．
若四边形CDQP为矩形，设Q（x，0），P（a，b），
∵∠CDQ=90°，
∴CD²+DQ²=CQ²，即4+3+x²=（x+1）²，
解得x=3，
∴Q（3，0），
∵CQ的中点坐标为（1，0），
∴线段PD的中点必是（1，0）
∴

a

2

=1，

3 +b

2

=0，
解得a=2，b=-

3

，
∴P（2，-

3

）．
∴点P（2，-

3

）满足反比例函数y=-

2 3

x

．

点评：本题考查的是反比例函数综合题，涉及到矩形的性质等知识，难度适中．