题目内容
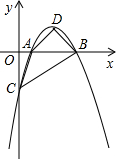
如图,已知直线y=2x+2交y轴于点A,交x轴于点B,直线l:y=-3x+9
(1)求经过A、B、C三点的抛物线的函数关系式,并指出此函数的函数值随x的增大而增大时,x的取值范围;
(2)若点E在(1)中的抛物线上,且四边形ABCE是以BC为底的梯形,求梯形ABCE的面积;
(3)在(1)、(2)的条件下,过E作直线EF⊥x轴,垂足为G,交直线l于F.在抛物线上是否存在点H,使直线l、FH和x轴所围成的三角形的面积恰好是梯形ABCE面积的
?若存在,求点H的横坐标;若不存在,请说明理由.

(1)求经过A、B、C三点的抛物线的函数关系式,并指出此函数的函数值随x的增大而增大时,x的取值范围;
(2)若点E在(1)中的抛物线上,且四边形ABCE是以BC为底的梯形,求梯形ABCE的面积;
(3)在(1)、(2)的条件下,过E作直线EF⊥x轴,垂足为G,交直线l于F.在抛物线上是否存在点H,使直线l、FH和x轴所围成的三角形的面积恰好是梯形ABCE面积的
| 1 |
| 2 |

(1)∵直线AB的解析式为y=2x+2,
∴点A、B的坐标分别为A(0,2)、B(-1,0);
又直线l的解析式为y=-3x+9,∴点C的坐标为(3,0).
由上,可设经过A、B、C三点的抛物线的解析式为y=a(x+1)(x-3),将点A的坐标代入,得:a=-
,
∴抛物线的解析式为y=-
x2+
x+2,
∴抛物线的对称轴为x=1;
由于抛物线的开口向下,所以函数值随x的增大而增大时,x的取值范围是x≤1.
(2)过A作AE∥BC,交抛物线于点E;显然,点A、E关于直线x=1对称,
∴点E的坐标为E(2,2);
故梯形ABCE的面积为 S=
(2+4)×2=6.
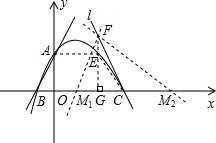 (3)假设存在符合条件的点H,作直线FH交x轴于M;
(3)假设存在符合条件的点H,作直线FH交x轴于M;
由题意知,S△CFM=3,设F(m,n),易知m=2;
将F(2,n)的坐标代入y=-3x+9中,可求出n=3,则FG=3;
∴S△CFM=
FG•CM=3,∴CM=2.
由C(3,0)知,M1(1,0)、M2(5,0),
设FM的解析式为y=kx+b:
由M1(1,0)、F(2,3)得,FM1解析式为y=3x-3,则FM1与抛物线的交点H满足:
,
整理得,2x2+5x-15=0,
∴x=
,
由M2(5,0)、F(2,3)得,FM2解析式为y=-x+5,则FM2与抛物线的交点H满足:
,整理得,2x2-7x+9=0,
∵△<0,∴不符合题意,舍去;
即:H点的横坐标为
.
∴点A、B的坐标分别为A(0,2)、B(-1,0);
又直线l的解析式为y=-3x+9,∴点C的坐标为(3,0).
由上,可设经过A、B、C三点的抛物线的解析式为y=a(x+1)(x-3),将点A的坐标代入,得:a=-
| 2 |
| 3 |
∴抛物线的解析式为y=-
| 2 |
| 3 |
| 4 |
| 3 |
∴抛物线的对称轴为x=1;
由于抛物线的开口向下,所以函数值随x的增大而增大时,x的取值范围是x≤1.
(2)过A作AE∥BC,交抛物线于点E;显然,点A、E关于直线x=1对称,
∴点E的坐标为E(2,2);
故梯形ABCE的面积为 S=
| 1 |
| 2 |
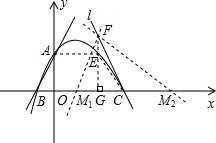 (3)假设存在符合条件的点H,作直线FH交x轴于M;
(3)假设存在符合条件的点H,作直线FH交x轴于M;由题意知,S△CFM=3,设F(m,n),易知m=2;
将F(2,n)的坐标代入y=-3x+9中,可求出n=3,则FG=3;
∴S△CFM=
| 1 |
| 2 |
由C(3,0)知,M1(1,0)、M2(5,0),
设FM的解析式为y=kx+b:
由M1(1,0)、F(2,3)得,FM1解析式为y=3x-3,则FM1与抛物线的交点H满足:
|
整理得,2x2+5x-15=0,
∴x=
-5±
| ||
| 4 |
由M2(5,0)、F(2,3)得,FM2解析式为y=-x+5,则FM2与抛物线的交点H满足:
|
∵△<0,∴不符合题意,舍去;
即:H点的横坐标为
-5±
| ||
| 4 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目