题目内容
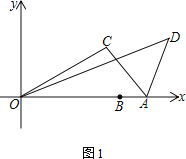
【题目】已知,点A(8,0)、B(6,0).将线段OB绕着原点O逆时针方向旋转角度α到OC,连接AC.将AC绕着点A顺时针方向旋转角度β至AD,连接OD
(1)当α=30°,β=60°时,求OD的长
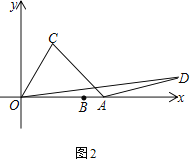
(2)当α=60°,β=120°时,求OD的长
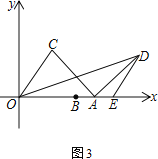
(3)已知E(10,0),当β=90°时,改变的大小,求ED的最大值
【答案】(1)![]() ;(2)
;(2)![]() ;(3)最大值为
;(3)最大值为![]()
【解析】
(1)将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 至
至![]() ,连接
,连接![]() ,
,![]() ,证明
,证明![]() ,再证明
,再证明![]() 后利用勾股定理求解即可;
后利用勾股定理求解即可;
(2)将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 至
至![]() ,连接
,连接![]() ,
,![]() ,证明
,证明![]() ,所以
,所以![]() .再证明
.再证明![]() ,利用勾股定理即可求出
,利用勾股定理即可求出![]() ;
;
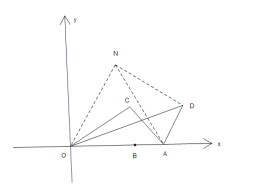
(3)将![]() 绕
绕![]() 顺时针旋转
顺时针旋转![]() 到
到![]() ,可得点N(8,8),利用两点间的距离公式可求出
,可得点N(8,8),利用两点间的距离公式可求出![]() ,当点D在线段NE上时,DE有最小值
,当点D在线段NE上时,DE有最小值![]() ,当D在线段NE的延长线上时,DE有最大值,最大值为
,当D在线段NE的延长线上时,DE有最大值,最大值为![]() .
.
解:(1)如图,将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 至
至![]() ,连接
,连接![]() ,
,![]() ,
,
则![]() 是等边三角形,
是等边三角形,
∴![]()
∴![]()
∴![]() ,即
,即![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]() ;
;
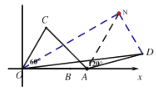
(2)如图,将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 至
至![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() 是等边三角形,
是等边三角形,
∵![]()
∴![]() ,
,![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∵∵![]()
∴![]()
∴![]() ;
;
(3)如图,将![]() 绕
绕![]() 顺时针旋转
顺时针旋转![]() 到
到![]() ,连接AN、DN、EN,可得点N(8,8),
,连接AN、DN、EN,可得点N(8,8),
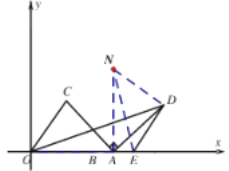
则![]()
由(1)得,![]()
∴![]()
∴当点D在线段NE上时,DE有最小值,最小值为:![]() ;
;
当D在线段NE的延长线上时,DE有最大值,最大值为:![]() ;
;
∴DE最大值为![]() .
.

练习册系列答案
相关题目
【题目】为了了解学生每月的零用钱情况,从甲、乙、丙三个学校各随机抽取200名学生,调查了他们的零用钱情况(单位:元)具体情况如下:
学校频数零用钱 | 100≤x<200 | 200≤x<300 | 300≤x<400 | 400≤x<500 | 500以上 | 合计 |
甲 | 5 | 35 | 150 | 8 | 2 | 200 |
乙 | 16 | 54 | 68 | 52 | 10 | 200 |
丙 | 0 | 10 | 40 | 70 | 80 | 200 |
在调查过程中,从__(填“甲”,“乙”或“丙”)校随机抽取学生,抽到的学生“零用钱不低于300元”的可能性最大.