题目内容
学了一元二次方程的根与系数的关系后,小亮兴奋地说:“若设一元二次方程的两个根为x1,x2,就能快速求出 ,…的值了.比如设x1,x2是方程x2+2x+3=0的两个根,则x1+x2=-2,x1x2=3,得
,…的值了.比如设x1,x2是方程x2+2x+3=0的两个根,则x1+x2=-2,x1x2=3,得 .”
.”(1)小亮的说法对吗?简要说明理由;
(2)写一个你最喜欢的一元二次方程,并求出两根的平方和.
【答案】分析:一般情况下可以这样计算 、x12+x22的值,但是若有一根为零时,就无法计算
、x12+x22的值,但是若有一根为零时,就无法计算 的值了.
的值了.
解答:解:(1)小亮的说法不对.
若有一根为零时,就无法计算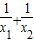 的值了,因为零作除数无意义.
的值了,因为零作除数无意义.
(2)所喜欢的一元二次方程x2-5x-6=0.
设方程的两个根分别为x1,x2,
∴x1+x2=5,x1•x2=-6.
又∵x12+x22=x12+x22+2x1x2-2x1x2=(x1+x2)2-2x1x2
将x1+x2=5,x1•x2=-6代入,得
x12+x22=(x1+x2)2-2x1x2
=52-2×(-6)
=37.
点评:将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.
 、x12+x22的值,但是若有一根为零时,就无法计算
、x12+x22的值,但是若有一根为零时,就无法计算 的值了.
的值了.解答:解:(1)小亮的说法不对.
若有一根为零时,就无法计算
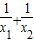 的值了,因为零作除数无意义.
的值了,因为零作除数无意义.(2)所喜欢的一元二次方程x2-5x-6=0.
设方程的两个根分别为x1,x2,
∴x1+x2=5,x1•x2=-6.
又∵x12+x22=x12+x22+2x1x2-2x1x2=(x1+x2)2-2x1x2
将x1+x2=5,x1•x2=-6代入,得
x12+x22=(x1+x2)2-2x1x2
=52-2×(-6)
=37.
点评:将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 ,…的值了.比如设x1,x2是方程x2+2x+3=0的两个根,则x1+x2=-2,x1x2=3,得
,…的值了.比如设x1,x2是方程x2+2x+3=0的两个根,则x1+x2=-2,x1x2=3,得 .”
.” ,…的值了.比如设x1,x2是方程x2+2x+3=0的两个根,则x1+x2=-2,x1x2=3,得
,…的值了.比如设x1,x2是方程x2+2x+3=0的两个根,则x1+x2=-2,x1x2=3,得 .”
.”