题目内容
【题目】已知:在平面直角坐标系中,点![]() ,点
,点![]() .
.
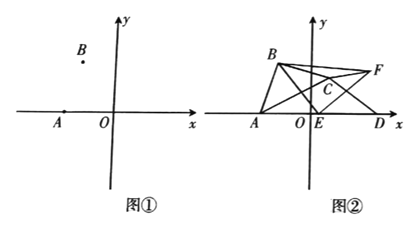
(1)在图①中的![]() 轴上求作点
轴上求作点![]() ,使得
,使得![]() 的值最小;
的值最小;
(2)若![]() 是以
是以![]() 为腰的等腰直角三角形,请直接写出点
为腰的等腰直角三角形,请直接写出点![]() 的坐标;
的坐标;
(3)如图②,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() (不与点
(不与点![]() 重合)是
重合)是![]() 轴上一个动点,点
轴上一个动点,点![]() 是
是![]() 中点,连结
中点,连结![]() ,把
,把![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() (即
(即![]() ,
,![]() ),连结
),连结![]() 、
、![]() 、
、![]() ,试猜想
,试猜想![]() 的度数,并给出证明.
的度数,并给出证明.
【答案】(1)见解析;(2)![]() ,
,![]() ,
,![]() ,
,![]() ;(3)45°,见解析
;(3)45°,见解析
【解析】
(1)作出点B关于y轴对称的点B1,连接AB1交y轴于点P,则P点即为所求;
(2)分别作出以AB为腰的等腰直角三角形,运用全等三角形的判定与性质求出点C的坐标即可;
(3)分点D运动到点A的右侧和左侧两种情形进行求解:①当点![]() 运动到点
运动到点![]() 右侧时,如图,延长
右侧时,如图,延长![]() 至
至![]() ,使
,使![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,首先证明
,首先证明![]() ≌
≌![]() 即可证明
即可证明![]() 是等腰直角三角形,进而证明
是等腰直角三角形,进而证明![]() ≌
≌![]() 可得
可得![]() ,
,![]() ,从而可得结论;②当点
,从而可得结论;②当点![]() 运动到点
运动到点![]() 左侧时,同理可得.
左侧时,同理可得.
(1)如图所示,
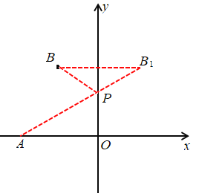
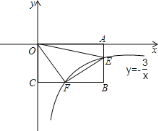
(2) 如图1,过点B作BD⊥x轴于点D,过点C作CE⊥BD于点E,
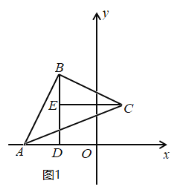
∵∠ABC=90°,
∴∠ABD+∠CBE=90°,
∵∠BAD+∠ABD=90°,
∴∠BAD=∠CBE,
在△BAD和△CBE中,
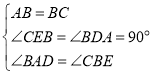
∴△BAD≌△CBE,
∴BE=AD,CE=BD,
∵A(-3,0),B(-2,3),
∴AD=1,BD=3,OD=2,
∴BE=1,DE=2,
∴C(1,2)
如图2,

易证△BAD≌△ACO,
∴OC=AD=1,
∴C(0,-1);
如图3,
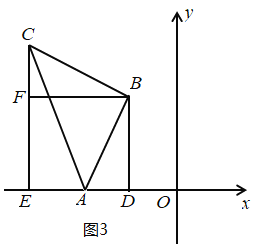
易证△BAD≌△BCF,
∴CF=AD=1,BF=ED=BD=3
∴CE=4,EO=5
∴C(-5,4);
如图4,
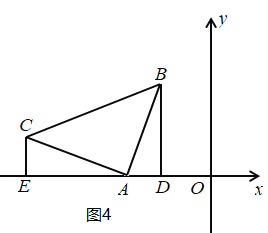
易证△BAD≌△CAE,
∴CE=AD=1,AE= BD=3
∴EO=6
∴C(-6,1);
故点C的坐标为:![]() ,
,![]() ,
,![]() ,
,![]()
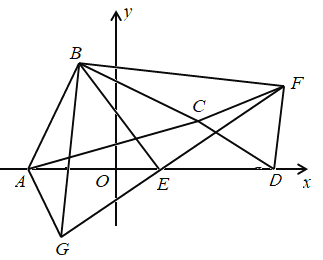
(3)猜想![]()
①当点![]() 运动到点
运动到点![]() 右侧时,
右侧时,
如图,延长![]() 至
至![]() ,使
,使![]() ,连结
,连结![]() ,
,![]() ,
,![]()
在![]() 和
和![]() 中
中
∵![]() ,
,![]() ,
,![]()
∴![]() ≌
≌![]() (
(![]() )
)
∴![]() ,
,![]()
∵![]()
∴![]()
∵![]() ,
,![]()
∴![]() 是等腰直角三角形
是等腰直角三角形
∴![]() ,
,![]() ,
,![]()
∵![]()
∴![]() ,
,
即![]()
∴![]()
在![]() 和
和![]() 中
中
∵![]() ,
,![]() ,
,![]()
∴![]() ≌
≌![]() (
(![]() )
)
∴![]() ,
,![]()
∵![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
![]() ∵
∵![]()
∴![]() 是等腰直角三角形,
是等腰直角三角形, ![]()
②当点![]() 运动到点
运动到点![]() 左侧时,同理可证,
左侧时,同理可证, ![]()
综上所述, ![]()

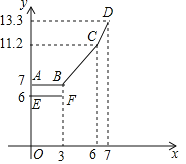
【题目】为缓解油价上涨给出租车待业带来的成本压力,某巿自2018年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超过3km的部分 | 起步价6元 | 起步价a 元 |
超过3km不超出6km的部分 | 每公里2.1元 | 每公里b元 |
超出6km的部分 | 每公里c元 | |
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元)如图,折线ABCD表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
(1)填空:a= ,b= ,c= .
(2)写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.
(3)函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义,若不存在请说明理由.