题目内容
下列说法:
①三角形的外心到三角形三边的距离相等.
②在直径为20的圆中,长为10的弦所对圆心角是30°
③垂直平分弦的直线必经过圆心
④平分弦的直径垂直于弦
⑤等弧所对的圆周角相等
其中正确的个数有( )
①三角形的外心到三角形三边的距离相等.
②在直径为20的圆中,长为10的弦所对圆心角是30°
③垂直平分弦的直线必经过圆心
④平分弦的直径垂直于弦
⑤等弧所对的圆周角相等
其中正确的个数有( )
分析:根据三角形的内心到三角形的三边的距离相等即可判断①,求出△OAB是等边三角形,根据等边三角形的性质即可判断②;根据垂径定理即可判断③;根据垂直平分弦(弦不是直径)的直径必经过圆心,即可判断④;等弧的前提条件是在
解答:解:∵三角形的外心到三角形的三个顶点的距离相等,三角形的内心到三角形的三边的距离相等,∴①错误;

如图,连接OA、OB,
∵OA=OB=
×20=10=AB,
∴△AOB是等边三角形,∴∠AOB=60°,∴②错误;
∵根据垂径定理可得:垂直平分弦的直线必经过圆心∴③正确;
∵如图,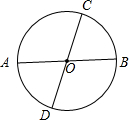
当AB是弦,CD是直径时,符合
CD平分AB,但CD不垂直AB,∴④错误;
圆周角定理的推论之一是:等弧所对的圆周角相等,∴⑤正确;
故选A.

如图,连接OA、OB,
∵OA=OB=
| 1 |
| 2 |
∴△AOB是等边三角形,∴∠AOB=60°,∴②错误;
∵根据垂径定理可得:垂直平分弦的直线必经过圆心∴③正确;
∵如图,

当AB是弦,CD是直径时,符合
CD平分AB,但CD不垂直AB,∴④错误;
圆周角定理的推论之一是:等弧所对的圆周角相等,∴⑤正确;
故选A.
点评:本题考查了垂径定理,三角形的外心和三角形的内心等知识点,主要考查学生的理解能力和辨析能力,题目比较好,但是一道比较容易出错的题目.

练习册系列答案
相关题目