题目内容
【题目】如图1,在△APE中,∠PAE=90°,PO是△APE的角平分线,以O为圆心,OA为半径作圆交AE于点G.
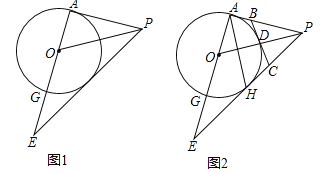
(1)求证:直线PE是⊙O的切线;
(2)在图2中,设PE与⊙O相切于点H,连结AH,点D是⊙O的劣弧![]() 上一点,过点D作⊙O的切线,交PA于点B,交PE于点C,已知△PBC的周长为4,tan∠EAH=
上一点,过点D作⊙O的切线,交PA于点B,交PE于点C,已知△PBC的周长为4,tan∠EAH=![]() ,求EH的长.
,求EH的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)作OH⊥PE,由PO是∠APE的角平分线,得到∠APO=∠EPO,判断出△PAO≌△PHO,得到OH=OA,用“圆心到直线的距离等于半径”来得出直线PE是⊙O的切线;
(2)先利用切线的性质和△PBC的周长为4求出PA=2,再用三角函数求出OA,AG,然后用三角形相似,得到EH=2EG,AE=2EH,用勾股定理求出EG,最后用切割线定理即可.
试题解析:(1)如图1,作OH⊥PE,∴∠OHP=90°,∵∠PAE=90,∴∠OHP=∠OAP,∵PO是∠APE的角平分线,∴∠APO=∠EPO,在△PAO和△PHO中,∵∠OHP=∠OAP,∠OPH=∠OPA,OP=OP,∴△PAO≌△PHO,∴OH=OA,∵OA是⊙O的半径,∴OH是⊙O的半径,∵OH⊥PE,∴直线PE是⊙O的切线.
(2)如图2,连接GH,∵BC,PA,PB是⊙O的切线,∴DB=DA,DC=CH,∵△PBC的周长为4,∴PB+PC+BC=4,∴PB+PC+DB+DC=4,∴PB+AB+PC+CH=4,∴PA+PH=4,∵PA,PH是⊙O的切线,∴PA=PH,∴PA=2,由(1)得,△PAO≌△PHO,∴∠OFA=90°,∴∠EAH+∠AOP=90°,∵∠OAP=90°,∴∠AOP+∠APO=90°,∴∠APO=∠EAH,∵tan∠EAH=![]() ,∴tan∠APO=
,∴tan∠APO=![]() =
=![]() ,∴OA=
,∴OA=![]() PA=1,∴AG=2,∵∠AHG=90°,∵tan∠EAH=
PA=1,∴AG=2,∵∠AHG=90°,∵tan∠EAH=![]() =
=![]() ,∵△EGH∽△EHA,∴
,∵△EGH∽△EHA,∴![]() =
=![]() =
=![]() ,∴EH=2EG,AE=2EH,∴AE=4EG,∵AE=EG+AG,∴EG+AG=4EG,∴EG=
,∴EH=2EG,AE=2EH,∴AE=4EG,∵AE=EG+AG,∴EG+AG=4EG,∴EG=![]() AG=
AG=![]() ,∵EH是⊙O的切线,EGA是⊙O的割线,∴
,∵EH是⊙O的切线,EGA是⊙O的割线,∴![]() =EG×EA=EG×(EG+AG)=
=EG×EA=EG×(EG+AG)=![]() =
=![]() ,∴EH=
,∴EH=![]() .
.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案