题目内容
【题目】如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别是OB,OD的中点.
(1)试说明四边形AECF是平行四边形.
(2)若AC=2,AB=1.若AC⊥AB,求线段BD的长.
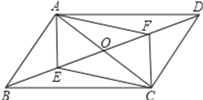
【答案】(1)见解析;(2)BD=2![]() .
.
【解析】
(1)在平行四边形ABCD中,AC与BD互相平分,OA=OC,OB=OD,又E,F为OB,OD的中点,所以OE=OF,所以AC与EF互相平分,所以四边形AECF为平行四边形;
(2)首先根据平行四边形的性质可得AO=CO,BO=DO,再利用勾股定理计算出BO的长,进而可得BD的长.
(1)证明:如图,
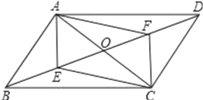
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E,F为OB,OD的中点,
∴OE=OF,
∴AC与EF互相平分,
∴四边形AECF为平行四边形;
(2)解:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵AC=2,
∴AO=2,
∵AB=1,AC⊥AB,
∴![]() ,
,
∴BD=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
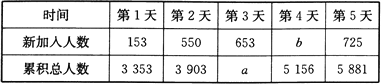
【题目】某报社为了了解市民“获取新闻的最主要途径”,开展了一次抽样调查,根据调查结果绘制了如下三种不完整的统计图表.
组别 | 获取新闻的最主要途径 | 人数 |
| 电脑上网 | 280 |
| 手机上网 |
|
| 电视 | 140 |
| 报纸 |
|
| 其他 | 80 |
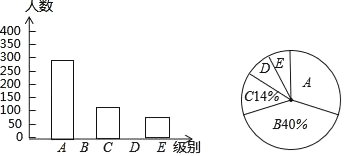
请根据图表信息解答下列问题:
(1)统计表中的![]() ,
,![]() ,并请补全条形统计图;
,并请补全条形统计图;
(2)扇形统计图中“![]() ”所对应的圆心角的度数是 ;
”所对应的圆心角的度数是 ;
(3)若该市约有100万人,请你估计其中将“电脑上网”和“手机上网”作为“获取新闻的最主要途径”的总人数.