题目内容
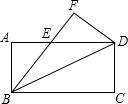
矩形ABCD沿对角线BD折叠，点C落在点F，若AB=2，BC=4，则BE的长是（ ）
A．
| B．
| C．2 | D．1 |
由折叠性质可知，∠EBD=∠CBD，
由矩形性质可知，∠EDB=∠CBD，
∴∠EBD=∠EDB，即BE=ED，设BE=x，则AE=4-x，
在Rt△ABE中，由勾股定理得：AB2+AE2=BE2，
即22+（4-x）2=x2，
解得x=
即BE=
．故选A．
由矩形性质可知，∠EDB=∠CBD，
∴∠EBD=∠EDB，即BE=ED，设BE=x，则AE=4-x，
在Rt△ABE中，由勾股定理得：AB2+AE2=BE2，
即22+（4-x）2=x2，
解得x=
| 5 |
| 2 |
| 5 |
| 2 |
练习册系列答案
相关题目
，折叠过程是这样的（阴影部分表示纸条的反面）：如果由信纸折成的长方形纸条（图①）长为26cm，宽为xcm，分别回答下列问题：
